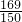题目内容
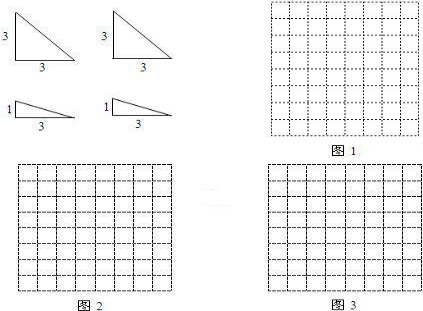
把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为( )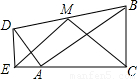
A.1
B.
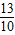
C.
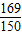
D.
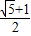
【答案】分析:过D作DF⊥BC于F,取EC的中点N,连接MN,得出四边形DECF是矩形,求出DF=EC=15,CF=DE=4,求出AB=15,AD=5,BD=5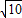 ,求出∠DAB=90°,求出△DAB的面积是
,求出∠DAB=90°,求出△DAB的面积是 ×AD×AB=
×AD×AB= ×5×15,根据梯形中位线得出MN∥DE,MN=
×5×15,根据梯形中位线得出MN∥DE,MN= (DE+BC)=
(DE+BC)= ,推出MN⊥EC,求出△MEC的面积是
,推出MN⊥EC,求出△MEC的面积是 ×EC×MN=
×EC×MN= ,代入求出即可.
,代入求出即可.
解答:解:
过D作DF⊥BC于F,取EC的中点N,连接MN,
∵∠DEA=∠BCE=∠DFC=90°,
∴四边形DECF是矩形,
∴DF=EC=3+12=15,CF=DE=4,
∴BF=9-4=5,
在Rt△BAC中,BC=9,AC=12,由勾股定理得:AB=15,
同理AD=5,
在Rt△DFB中,DF=15,BF=5,由勾股定理得BD=5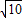 ,
,
∵AD=5,AB=15,
∴AD2+AB2=25+225=250,BD2=250,
∴AD2+AB2=BD2,
∴∠DAB=90°,
即△DAB的面积是 ×AD×AB=
×AD×AB= ×5×15,
×5×15,
∵∠DEA=∠BCE=90°,
∴DE∥BC,
∵M为BD中点,N为EC中点,
∴MN∥DE,MN= (DE+BC)=
(DE+BC)= ×(4+9)=
×(4+9)= ,
,
∴MN⊥EC,
∴△MEC的面积是 ×EC×MN=
×EC×MN= ×(3+12)×
×(3+12)× =
=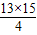 ,
,
∴△EMC与△DAB面积的比是( ×5×15):
×5×15):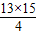 =13:10,
=13:10,
故选B.
点评:本题考查了梯形的性质,梯形的中位线,三角形的面积,等腰直角三角形等知识点的应用,通过做此题培养了学生运用定理进行计算的能力,题目比较好,但有一定的难度.
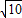 ,求出∠DAB=90°,求出△DAB的面积是
,求出∠DAB=90°,求出△DAB的面积是 ×AD×AB=
×AD×AB= ×5×15,根据梯形中位线得出MN∥DE,MN=
×5×15,根据梯形中位线得出MN∥DE,MN= (DE+BC)=
(DE+BC)= ,推出MN⊥EC,求出△MEC的面积是
,推出MN⊥EC,求出△MEC的面积是 ×EC×MN=
×EC×MN= ,代入求出即可.
,代入求出即可.解答:解:

过D作DF⊥BC于F,取EC的中点N,连接MN,
∵∠DEA=∠BCE=∠DFC=90°,
∴四边形DECF是矩形,
∴DF=EC=3+12=15,CF=DE=4,
∴BF=9-4=5,
在Rt△BAC中,BC=9,AC=12,由勾股定理得:AB=15,
同理AD=5,
在Rt△DFB中,DF=15,BF=5,由勾股定理得BD=5
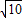 ,
,∵AD=5,AB=15,
∴AD2+AB2=25+225=250,BD2=250,
∴AD2+AB2=BD2,
∴∠DAB=90°,
即△DAB的面积是
 ×AD×AB=
×AD×AB= ×5×15,
×5×15,∵∠DEA=∠BCE=90°,
∴DE∥BC,
∵M为BD中点,N为EC中点,
∴MN∥DE,MN=
 (DE+BC)=
(DE+BC)= ×(4+9)=
×(4+9)= ,
,∴MN⊥EC,
∴△MEC的面积是
 ×EC×MN=
×EC×MN= ×(3+12)×
×(3+12)× =
=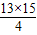 ,
,∴△EMC与△DAB面积的比是(
 ×5×15):
×5×15):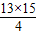 =13:10,
=13:10,故选B.
点评:本题考查了梯形的性质,梯形的中位线,三角形的面积,等腰直角三角形等知识点的应用,通过做此题培养了学生运用定理进行计算的能力,题目比较好,但有一定的难度.

练习册系列答案
相关题目

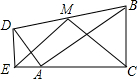 (2012•拱墅区一模)把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为( )
(2012•拱墅区一模)把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为( )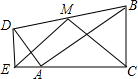 把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为
把两个直角边长分别为3、4与9、12的Rt△ADE和Rt△ABC按照如图所示的位置放置,已知DE=4,AC=12,且E,A,C三点在同一直线上,连接BD,取BD的中点M,连接ME,MC,则△EMC与△DAB面积的比值为