题目内容
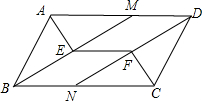 (2008•顺义区二模)已知:如图,平行四边形ABCD中,AE、BE、CF、DF分别平分∠BAD、∠ABC、∠BCD、∠CDA,BE、DF的延长线分别交AD、BC于点M、N,连接EF,若AD=7,AB=4,求EF的长.
(2008•顺义区二模)已知:如图,平行四边形ABCD中,AE、BE、CF、DF分别平分∠BAD、∠ABC、∠BCD、∠CDA,BE、DF的延长线分别交AD、BC于点M、N,连接EF,若AD=7,AB=4,求EF的长.分析:根据平行四边形的性质和角平分线的定义先证明AM=AB=4,再利用已知条件证明四边形BNDM是平行四边形,进而得到BM=DN,BM∥DN,所以四边形MEFD也是平行四边形,再利用平行四边形的性质:对边相等即可求出DM的长,所以也就求出EF的长.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=CD.
∴∠2=∠3.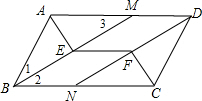
∵BE平分∠ABC,
∴∠1=∠2.
∴∠1=∠3.
∴AM=AB=4.
∵AE平分∠BAD,
∴EM=
BM,
.同理,CN=CD,DF=
DN,
∴AM=CN.
∴AD-AM=BC-CN,即 DM=BN.
∴四边形BNDM是平行四边形,
∴BM=DN,BM∥DN.
∴EM=DF,EM∥DF.
∴四边形MEFD是平行四边形.
∴EF=MD.
∵DM=AD-AM=AD-AB=7-4=3,
∴EF=DM=3.
∴AD∥BC,AD=BC,AB=CD.
∴∠2=∠3.

∵BE平分∠ABC,
∴∠1=∠2.
∴∠1=∠3.
∴AM=AB=4.
∵AE平分∠BAD,
∴EM=
| 1 |
| 2 |
.同理,CN=CD,DF=
| 1 |
| 2 |
∴AM=CN.
∴AD-AM=BC-CN,即 DM=BN.
∴四边形BNDM是平行四边形,
∴BM=DN,BM∥DN.
∴EM=DF,EM∥DF.
∴四边形MEFD是平行四边形.
∴EF=MD.
∵DM=AD-AM=AD-AB=7-4=3,
∴EF=DM=3.
点评:本题考查了平行四边形的性质和判定以及角平分线的定义,题目的难度中等.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 (2008•顺义区二模)如图,AB是⊙O的直径,AC是弦,若AB=2,AC=
(2008•顺义区二模)如图,AB是⊙O的直径,AC是弦,若AB=2,AC=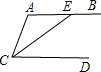 (2008•顺义区二模)已知:如图,AB∥CD,CE平分∠ACD,交AB于点E,若∠A=110°,则∠BEC的度数是
(2008•顺义区二模)已知:如图,AB∥CD,CE平分∠ACD,交AB于点E,若∠A=110°,则∠BEC的度数是