题目内容
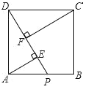
【题目】如图,在正方形ABCD中,点P在AB边上,AE⊥DP于E点,CF⊥DP于F点,若AE=5,CF=9,则EF=_______.
【答案】4
【解析】
由正方形的性质可得CD=DA,∠CDA=90°,由余角的性质可得∠DCF=∠ADE,进而可用AAS证明△CDF≌△DAE,然后根据全等三角形的性质和线段的和差关系即可求出结果.
解:∵四边形ABCD是正方形,
∴CD=DA,∠CDA=90°,
∵AE⊥DP于E点,CF⊥DP于F点,
∴∠CFD=∠AED=90°,
∵∠FDC+∠DCF=90°,∠CDF+∠ADE=90°,
∴∠DCF=∠ADE,
∴△CDF≌△DAE(AAS).
∴DE=CF=9,DF=AE=5,
∴EF=DE﹣DF=9﹣5=4.
故答案为:4.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
3 km | 10 km | -4 km | -3 km | -7 km |
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)该驾驶员离公司距离最远是多少千米?
(3)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?