题目内容
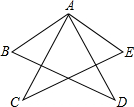已知如图：AC=AD，∠B=∠E，∠BAC=∠EAD，则EC=BD吗？说明理由．分析：首先根据∠BAC=∠EAD得到∠BAD=∠EAC，然后利用ASA即可证得△ABD≌△EAC，根据全等三角形的对应边相等即可证得CE=BD．
解答：解：CE=BD．
证明：∵∠BAC=∠EAD，
∴∠BAC+∠CAD=∠EAD+∠CAD，即∠BAD=∠EAC，
在△ABD和△EAC中，
，
∴△ABD≌△EAC（ASA），
∴CE=BD．
证明：∵∠BAC=∠EAD，
∴∠BAC+∠CAD=∠EAD+∠CAD，即∠BAD=∠EAC，
在△ABD和△EAC中，
|
∴△ABD≌△EAC（ASA），
∴CE=BD．
点评：本题考查了全等三角形的判定与性质，注意证明全等的条件是：三角形的边相等，角相等．
练习册系列答案
相关题目
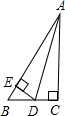已知如图，AC⊥BC，DE⊥AB，AD平分∠BAC，下面结论错误的是（ ）| A、BD+ED=BC | B、DE平分∠ADB | C、AD平分∠EDC | D、ED+AC＞AD |
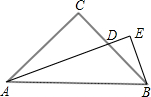
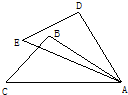
15、已知如图，AC=AE，AB=AD，∠CAE=∠BAD．求证：BC=DE．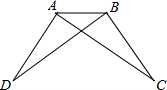
已知如图，AC=BD，AD⊥AC，BD⊥BC，求证：AD=BC．