题目内容
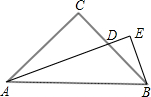
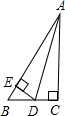 已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
已知如图,AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )| A、BD+ED=BC | B、DE平分∠ADB | C、AD平分∠EDC | D、ED+AC>AD |
分析:根据角平分线上的点到角的两边的距离相等可得DE=DC,然后利用AAS证明△ACD≌△AED,再对各选项分析判断后利用排除法.
解答:解:∵AC⊥BC,DE⊥AB,AD平分∠BAC,
∴DE=DC,
A、BD+ED=BD+DC=BC,故本选项正确;
B、C、在△ACD与△AED中,
,
∴△ACD≌△AED(AAS),
∴∠ADC=∠ADE,
∴AD平分∠EDC,故C选项正确;
但∠ADE与∠BDE不一定相等,故B选项错误;
D、∵△ACD≌△AED,
∴AE=AC,
∴ED+AC=ED+AE>AD(三角形任意两边之和大于第三边),故本选项正确.
故选B.
∴DE=DC,
A、BD+ED=BD+DC=BC,故本选项正确;
B、C、在△ACD与△AED中,
|
∴△ACD≌△AED(AAS),
∴∠ADC=∠ADE,
∴AD平分∠EDC,故C选项正确;
但∠ADE与∠BDE不一定相等,故B选项错误;
D、∵△ACD≌△AED,
∴AE=AC,
∴ED+AC=ED+AE>AD(三角形任意两边之和大于第三边),故本选项正确.
故选B.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,证明△ACD≌△AED是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
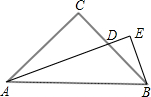
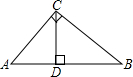 已知如图:AC⊥BC,CD⊥AB,则点B到AC的距离是线段
已知如图:AC⊥BC,CD⊥AB,则点B到AC的距离是线段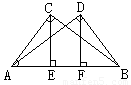
 AD.
AD.