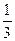题目内容
. 试写一个有两个不相等实根的一元二次方程:

根据根与系数的关系,一元二次方程有两个不相等的实根,则必须满足△=b2-4ac>0,可结合以上条件,写出满足条件的一元二次方程;
解:要使一元二次方程有两个不相等的实根,则必须满足△=b2-4ac>0,
∵假设x2+4x-5=0,则△=b2-4ac=16-(-4×5)=36>0;
∴一元二次方程x2+4x-5=0,有两个不相等的实根.
故答案为:x2+4x-5=0(答案不唯一).
解:要使一元二次方程有两个不相等的实根,则必须满足△=b2-4ac>0,
∵假设x2+4x-5=0,则△=b2-4ac=16-(-4×5)=36>0;
∴一元二次方程x2+4x-5=0,有两个不相等的实根.
故答案为:x2+4x-5=0(答案不唯一).

练习册系列答案
相关题目
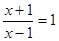
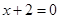


 市为争创全国文明卫生城,2008年市政府对市区绿化工程投
市为争创全国文明卫生城,2008年市政府对市区绿化工程投