Question

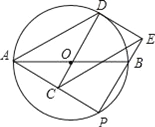
【题目】如图，AB是⊙O的直径，点P是AB下方的半圆上不与点A，B重合的一个动点，点C为AP中点，延长CO交⊙O于点D，连接AD，过点D作⊙O的切线交PB的廷长线于点E，连CE交AB于点F，连接DF．

（1）求证：△DAC≌△ECP；

（2）填空：

①四边形ACED是何种特殊的四边形？

②在点P运动过程中，线段DF、AP的数量关系是　 　．

Answer 1

【答案】（1）证明见解析；（2）①四边形ACED是平行四边形；②DF=AP，

【解析】

（1）由已知条件易得∠CDE=∠DCA=∠DCP=∠P=90°，由此可得四边形DCPE是矩形，从而可得DC=EP，这样结合AC=PC即可由“SAS”证得△DAC≌△ECP；

（2）①由（1）中所得△DAC≌△ECP可得AD=CE，∠DAC=∠ECP，从而可得AD∥CE，由此即可得到四边形ACED是平行四边形；②由OA=OD,AD∥CE易得∠DAO=∠ADC=∠DCF，由此可得A、C、F、D四点共圆，结合∠DAF=∠ADC可得在该圆中弦DF=AC，结合点C是AP的中点即可得到DF=AP.

（1）∵DE为切线，

∴OD⊥DE，

∴∠CDE=90°，

∵点C为AP的中点，

∴DC⊥AP，

∴∠DCA=∠DCP=90°，

∵AB是⊙O直径，

∴∠APB=90°，

∴四边形DEPC为矩形，

∴DC=EP，

∵在△DAC和△ECP中：，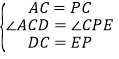

∴△DAC≌△ECP；

（2）①∵△DAC≌△ECP，

∴AD=CE，∠DAC=∠ECP，

∴AD∥CE，

∴四边形ACED是平行四边形；

②∵OA=OD，

∴∠DAF=∠ADC，

∵AD∥CE，

∴∠ADC=∠DCF，

∴∠DAF=∠DCF，

∴A，C，F，D四点共圆，

又∵∠ADF=∠ADC，

∴AC=DF，

∵AC=AP，

∴DF=AP.