题目内容
【题目】如图，在△ABC中，∠A=70°，AC=BC ， 以点B为旋转中心把△ABC按顺时针旋转α度，得到△A′B′C ， 点A′恰好落在AC上，连接CC′，则∠ACC′=.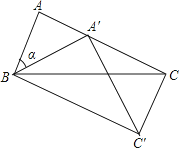
【答案】110°
【解析】∵∠A=70°，AC=BC ，
∴∠BCA=40°，
根据旋转的性质，AB=BA′，BC=BC′，
∴∠α=180°-2×70°=40°，
∵∠CBC′=∠α=40°，
∴∠BCC′=70°，
∴∠ACC′=∠ACB+∠BCC′=110°；
所以答案是：110°．
【考点精析】认真审题，首先需要了解旋转的性质(①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了)．
练习册系列答案
阅读快车系列答案
相关题目
