题目内容
【题目】 在Rt△ABC中,∠C=90°,AC=3,BC=5.作一边的垂直平分线交另一边于点D,则CD的长是______.
【答案】![]() 或
或![]()
【解析】
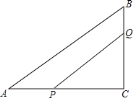
分两种情况:①当作斜边AB的垂直平分线PQ,与BC交于点D时,连接AD由PQ垂直平分线段AB,推出DA=DB,设DA=DB=x,在Rt△ACD中,∠C=90°,根据AD2=AC2+CD2构建方程即可解决问题;②当作直角边的垂直平分线PQ,与斜边AB交于点D时,连接CD,根据直角三角形斜边上的中线性质求得CD.
解:当作斜边AB的垂直平分线PQ,与BC交于点D时,连接AD.
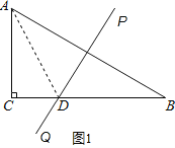
∵PQ垂直平分线段AB,
∴DA=DB,设DA=DB=x,
在Rt△ACD中,∠C=90°,AD2=AC2+CD2,
∴x2=32+(5-x)2,
解得x=![]() ,
,
∴CD=BC-DB=5-![]() =
=![]() ;
;
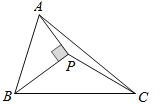
当作直角边的垂直平分线PQ或P′Q′,都与斜边AB交于点D时,连接CD,
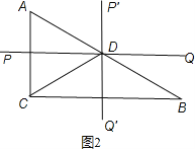
则D是AB的中点,
∴CD=![]() AB=
AB=![]() ,
,
综上可知,CD=![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目
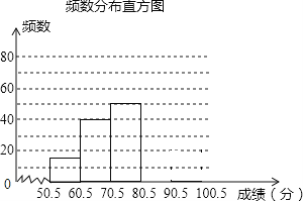
【题目】 某校为加强学生安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)进行统计,请根据尚为完成的频率和频数分布直方图,解答下列问题:
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了______名学生的竞赛成绩进行统计,其中m=______,n=______;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?