题目内容
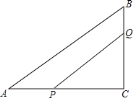
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点出发向点
点出发向点![]() 以
以![]() 的速度移动,点
的速度移动,点![]() 从
从![]() 点出发向点
点出发向点![]() 以
以![]() 的速度移动,当其中一点首先到达终点时运动停止,若
的速度移动,当其中一点首先到达终点时运动停止,若![]() 、
、![]() 分别同时从
分别同时从![]() ,
,![]() 出发,几秒后四边形
出发,几秒后四边形![]() 是
是![]() 面积的
面积的![]() ?
?
【答案】点![]() ,
,![]() 出发
出发![]() 秒后可使四边形
秒后可使四边形![]() 是
是![]() 面积的
面积的![]() .
.
【解析】
由于四边形APQB是一个不规则的图形,不容易表示它的面积,观察图形,可知S四边形APQB=S△ABC﹣S△PCQ,因此当四边形APQB是△ABC面积的![]() 时,△PCQ是△ABC面积的
时,△PCQ是△ABC面积的![]() ,即有S△PCQ=
,即有S△PCQ=![]() S△ABC.
S△ABC.
△ABC中,∵∠C=90°,∴△ABC是直角三角形,由勾股定理,得:BC=![]() =6.
=6.
设t秒后四边形APQB是△ABC面积的![]() ,则t秒后,CQ=BC﹣BQ=6﹣t,PC=AC﹣AP=8﹣2t.
,则t秒后,CQ=BC﹣BQ=6﹣t,PC=AC﹣AP=8﹣2t.
根据题意,知S△PCQ=![]() S△ABC,∴
S△ABC,∴![]() CQ×PC=
CQ×PC=![]() ×
×![]() AC×BC,即
AC×BC,即![]() (6﹣t)(8﹣2t)=
(6﹣t)(8﹣2t)=![]() ×
×![]() ×8×6,解得:t=2或t=8(舍去).
×8×6,解得:t=2或t=8(舍去).
答:点P,Q出发2秒后可使四边形APQB是△ABC面积的![]() .
.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】抛物线y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
x | … | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| … |
y | … | ﹣ | ﹣2 | ﹣ | ﹣2 | ﹣ | 0 |
| … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,﹣2);
③抛物线的对称轴是:x=1;
④在对称轴左侧,y随x增大而增大.
A. 1 B. 2 C. 3 D. 4