题目内容
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
| 2 |
分析:由题意即可推出A点的坐标,把A点的坐标代入到函数表达式,即可推出k的值.
解答: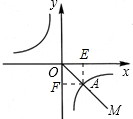 解:如图,作AE垂直于x轴,作AF垂直于y轴,
解:如图,作AE垂直于x轴,作AF垂直于y轴,
∵OM平分∠EOF,
∴∠EOM=45°,
∵OA=3
,
∴OE=AE=3,
∵A点在第四象限,
∴A(3,-3),
∵y=
(k≠0),
∴-3=
,
解得:k=-9.
故答案为:-9.
 解:如图,作AE垂直于x轴,作AF垂直于y轴,
解:如图,作AE垂直于x轴,作AF垂直于y轴,∵OM平分∠EOF,
∴∠EOM=45°,
∵OA=3
| 2 |
∴OE=AE=3,
∵A点在第四象限,
∴A(3,-3),
∵y=
| k |
| x |
∴-3=
| k |
| 3 |
解得:k=-9.
故答案为:-9.
点评:本题主要考查等腰直角三角形的性质,反比例函数的性质,关键在于作辅助线,求出A点的坐标.

练习册系列答案
相关题目
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
| 18 |
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
A、y=
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
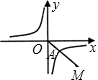 如图,第四象限的角平分线OM与反比例函数
如图,第四象限的角平分线OM与反比例函数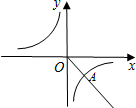 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=