题目内容
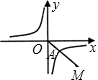 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k | x |
分析:此题关键是求得点A的坐标,根据第四象限的角平分线上的点的横、纵坐标互为相反数,结合OA的长,根据勾股定理即可求得;再设y=
,把点A的坐标代入可求出k值,即得到反比例函数的解析式.
| k |
| x |
解答: 解:设反比例函数解析式为:y=
解:设反比例函数解析式为:y=
,
根据题意,可设A(x,-x)(x>0).
∵OA=3,
∴x2+(-x)2=9
x=
.
∴点A的坐标为(
,-
),
则有k=
×(-
)=-
,
所以y=-
.
故答案为:y=
.
 解:设反比例函数解析式为:y=
解:设反比例函数解析式为:y=| k |
| x |
根据题意,可设A(x,-x)(x>0).
∵OA=3,
∴x2+(-x)2=9
x=
3
| ||
| 2 |
∴点A的坐标为(
3
| ||
| 2 |
3
| ||
| 2 |
则有k=
3
| ||
| 2 |
3
| ||
| 2 |
| 9 |
| 2 |
所以y=-
| 9 |
| 2x |
故答案为:y=
| 9 |
| 2x |
点评:此题主要考查了用待定系数法求反比例函数的解析式的方法.注意:第四象限角平分线上的点的横、纵坐标互为相反数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
| 18 |
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
A、y=
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
 如图,第四象限的角平分线OM与反比例函数
如图,第四象限的角平分线OM与反比例函数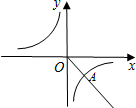 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=