题目内容
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
| 18 |
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
分析:可设点A的坐标为(x,-x),根据OA的长为
可得x2的值,反比例函数的比例系数为-x2.
| 18 |
解答: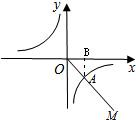 解:作AB⊥x轴于点B,设点A的坐标为(x,-x),
解:作AB⊥x轴于点B,设点A的坐标为(x,-x),
∴x2+(-x)2=18,
x2=9,
∴反比例函数的比例系数为-x2=-9,
∴y=-
,
故选C.
 解:作AB⊥x轴于点B,设点A的坐标为(x,-x),
解:作AB⊥x轴于点B,设点A的坐标为(x,-x),∴x2+(-x)2=18,
x2=9,
∴反比例函数的比例系数为-x2=-9,
∴y=-
| 9 |
| x |
故选C.
点评:考查一次函数与反比例函数的交点问题;用到的知识点为:第四象限角平分线上的点的横纵坐标互为相反数.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=| k |
| x |
A、y=
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-
|
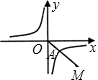 如图,第四象限的角平分线OM与反比例函数
如图,第四象限的角平分线OM与反比例函数 如图,第四象限的角平分线OM与反比例函数
如图,第四象限的角平分线OM与反比例函数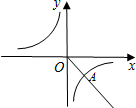 如图,第四象限的角平分线OM与反比例函数y=
如图,第四象限的角平分线OM与反比例函数y=