题目内容
泰州新星电子科技公司积极应对世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?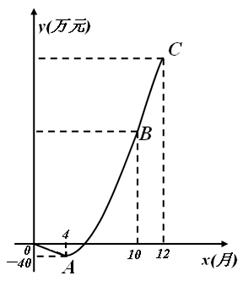
 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?

(1)设直线OA的解析式为y=kx,
∵点O(0,0),A(4,-40)在该直线上,
∴-40=4k,
解得k=-10,
∴y=-10x;
∵点B在抛物线y=-5x2+205x-1230上,
设B(10,m),则m=320.
∴点B的坐标为(10,320).
∵点A为抛物线的顶点,
∴设曲线AB所在的抛物线的解析式为y=a(x-4)2-40,
∴320=a(10-4)2-40,
解得a=10,
即y=10(x-4)2-40=10x2-80x+120.
∴y=-10x(x=1、2、3、4)
y=10x2-80x+120(x=5、6、7、8、9)
y=-5x2+205x-1230(x=10、11、12)
(2)利用第x+1个月的利润应该是前x+1个月的利润之和减去前x个月的利润之和:
-10(x+1)-[-(10x)](x=1、2、3、4)
10(x+1)2-80(x+1)+120-[10x2-80x+120](x=5、6、7、8、9)
-5(x+1)2+205(x+1)-1230-(-5x2+205x-1230)(x=10、11、12)
即S=-10(x=1、2、3、4)
S=20x-90(x=5、6、7、8、9)
S=-10x+210(x=10、11、12)
(3)由(2)知当x=1,2,3,4时,s的值均为-10,
当x=5,6,7,8,9时,当x=9时s有最大值90,
而在x=10,11,12时,s=-10x+210,
当x=10时,s有最大值110,
因此第9月公司所获利润最大,它是110万元.
∵点O(0,0),A(4,-40)在该直线上,
∴-40=4k,
解得k=-10,
∴y=-10x;
∵点B在抛物线y=-5x2+205x-1230上,
设B(10,m),则m=320.
∴点B的坐标为(10,320).
∵点A为抛物线的顶点,
∴设曲线AB所在的抛物线的解析式为y=a(x-4)2-40,
∴320=a(10-4)2-40,
解得a=10,
即y=10(x-4)2-40=10x2-80x+120.
∴y=-10x(x=1、2、3、4)
y=10x2-80x+120(x=5、6、7、8、9)
y=-5x2+205x-1230(x=10、11、12)
(2)利用第x+1个月的利润应该是前x+1个月的利润之和减去前x个月的利润之和:
-10(x+1)-[-(10x)](x=1、2、3、4)
10(x+1)2-80(x+1)+120-[10x2-80x+120](x=5、6、7、8、9)
-5(x+1)2+205(x+1)-1230-(-5x2+205x-1230)(x=10、11、12)
即S=-10(x=1、2、3、4)
S=20x-90(x=5、6、7、8、9)
S=-10x+210(x=10、11、12)
(3)由(2)知当x=1,2,3,4时,s的值均为-10,
当x=5,6,7,8,9时,当x=9时s有最大值90,
而在x=10,11,12时,s=-10x+210,
当x=10时,s有最大值110,
因此第9月公司所获利润最大,它是110万元.
(1)根据各段图象所过的特殊点易求其解析式,注意自变量的取值范围,综合起来得结论;
(2)在各段中,s=yx-y(x-1);
(3)根据函数性质分别求出各段中s的最大值比较后得结论.
(2)在各段中,s=yx-y(x-1);
(3)根据函数性质分别求出各段中s的最大值比较后得结论.

练习册系列答案
相关题目
 经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m,
经过点O、A、B三点,且A点坐标为(4,0),B的坐标为(m, ),点C是抛物线在第三象限的一点,且横坐标为-2.
),点C是抛物线在第三象限的一点,且横坐标为-2.
 的图象经过
的图象经过 和
和 两点,且交
两点,且交 轴于点
轴于点 .
. 、
、 的值;
的值; 轴交抛物线于点
轴交抛物线于点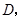 点
点 为此抛物线的顶点,试确定
为此抛物线的顶点,试确定 的形状.
的形状.

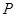 为抛物线
为抛物线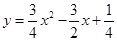 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点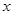 轴上方,过点
轴上方,过点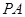 垂直
垂直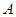 ,
,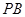 垂直
垂直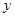 轴于点
轴于点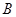 ,得到矩形
,得到矩形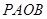 .若
.若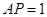 ,求矩形
,求矩形
 的y与x的部分对应值如下表:
的y与x的部分对应值如下表: 的正根在3与4之间
的正根在3与4之间 ,下列说法正确的是( )
,下列说法正确的是( )

 的顶点坐标是 ,x 时,y随x的增大而增大.
的顶点坐标是 ,x 时,y随x的增大而增大.



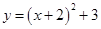 的顶点坐标是 【 】
的顶点坐标是 【 】