题目内容
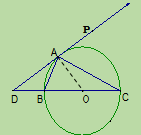
【题目】如图所示, ![]() 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.
【答案】
(1)
证明:连接AO,易知:
△ABO是等边三角形,AB=BD=1;
∴∠ADC=∠DAC=![]() ∠ABO=30°,而∠AOC=60°;
∠ABO=30°,而∠AOC=60°;
∴∠DAO=90°
∴DA是⊙o的切线;
(2)
解:当点P运动到A处时,即DP=DA=![]() 时,∠BPC的度数达到最大,最大值为90°.理由如下:
时,∠BPC的度数达到最大,最大值为90°.理由如下:
若点P不在A处时,不妨设点P在DA的延长线上,连接BP,与⊙o交于一点,记为点E,连接CE,
∴∠BPC<∠BEC=∠BAC=90°;
(3)
解:作点C关于射线DA的对称点C′,则BP+PC=BP+PC′,当点C′,P,B三点共线时,(PB+PC)的值达到最小,最小为BC.
过点作DC的垂线,垂足记为点H,连接DC′;
在RT△DCP中,∠PDC=30°;
∴△DCC′为等边三角形,
∴H为DC的中点,
∴BH=DH-DB=![]() CD-DB=
CD-DB=![]() -1=
-1=![]() ;
;
∴C′H=![]() DH=
DH=![]() ;
;
由勾股定理求出:BC′=![]() ;
;
∴(PB+PC)的最小值为![]() ;
;
【解析】(1)连接AO,易知:△ABO是等边三角形,通过计算可以得出∠DAO=90°,所以DA是⊙o的切线;
(2)当点P运动到A处时,即DP=DA= 时,∠BPC的度数达到最大,最大值为90°.理由如下:若点P不在A处时,不妨设点P在DA的延长线上,连接BP,与⊙o交于一点,记为点E,连接CE,所以∠BPC<∠BEC=∠BAC=90°;
(3)作点C关于射线DA的对称点C′,则BP+PC=BP+PC′,当点C′,P,B三点共线时,(PB+PC)的值达到最小,最小为BC.过点作DC的垂线,垂足记为点H,连接DC;通过等边三角形的性质和勾股定理即可求出。
【考点精析】关于本题考查的两点间的距离和等边三角形的性质,需要了解同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记;等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

 期末集结号系列答案
期末集结号系列答案




