Question

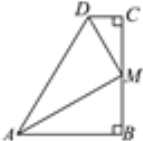
【题目】如图所示，已知∠B＝∠C＝90°，AM平分∠DAB，DM平分∠ADC.

(1)求证：M是BC的中点.

(2) 求证：AD＝AB＋CD.

(3)S△AMD=______S四边形ABCD.

Answer 1

【答案】（1）见解析；（2）见解析；（3）.

【解析】

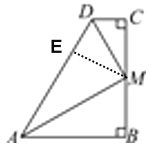
（1）过点M作ME⊥AD交AD于点E，根据角平分线的性质定理可得ME=MB，ME=MC，等量代换得到MB=MC即可证明；

（2）利用HL易证Rt△AEM≌Rt△ABM，Rt△DCM≌Rt△DEM，可得AD＝AE＋DE＝AB＋CD；

（3）利用三角形全等的性质得到S△AEM＝S△ABM，S△DCM＝S△DEM，即可求出S△AMD＝S△AEM＋S△DEM＝S四边形ABCD.

解：（1）过点M作ME⊥AD交AD于点E，

∵∠B＝∠C＝90°，

∴MB⊥AB，MC⊥DC，

又∵AM平分∠DAB，DM平分∠ADC，ME⊥AE，ME⊥DE，

∴ME=MB，ME=MC，

∴MB=MC，即M是BC的中点；

（2）在Rt△AEM和Rt△ABM中，，

∴Rt△AEM≌Rt△ABM（HL），

∴AE=AB，

同理可证Rt△DCM≌Rt△DEM，

∴DC=DE，

∴AD＝AE＋DE＝AB＋CD；

（3）由（2）可知Rt△AEM≌Rt△ABM，Rt△DCM≌Rt△DEM，

∴S△AEM＝S△ABM，S△DCM＝S△DEM，

∴S△AMD＝S△AEM＋S△DEM＝S四边形ABCD.