题目内容
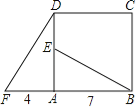
【题目】我市侯镇二中校园内有一荷花池,荷花池北侧有一水塔.九年级数学兴趣小组欲利用所学知识测量水塔高度.测量过程如下:先在荷花池南侧A点由测角仪AE测得塔顶仰角为30°,再在荷花池北侧B点由测角仪BF测得塔顶仰角为45°,荷花池AB长为15米,测角仪高均为1.5米,已知A、B、C三点在一条直线上,请根据以上条件求塔高CD?(保留两位小数)

【答案】21.75m;
【解析】
首先证明FG=DG═x(m),在Rt△BCM中,利用勾股定理求出GD即可解决问题.
根据题意得:BF=AE=GC=1.5m,EF=AB=15m,
设DG=x,
在Rt△DFG中,∠DFG=45°,
∴FG=DG═x(m),
在Rt△DEG中,EG=![]() x(m),
x(m),
∵EG﹣FG=15
∴![]() x﹣x=15,
x﹣x=15,
解得:x=![]() ≈20.25(m),
≈20.25(m),
∴CD=DG+CG =20.25+1.5=21.75(m),
答:塔高约为21.75m.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30