题目内容
如图,矩形ABCD中,边长AB=3,tan∠ABD=| 4 | 3 |
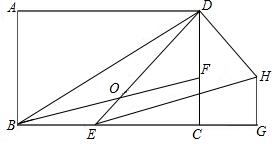 (1)若BE=1,求DH的长;
(1)若BE=1,求DH的长;(2)当E点在BC边上的什么位置时,△BOE与△DOF的面积相等?
(3)延长DH交BC的延长线于M,当E点在BC边上的什么位置时,DM=DE?
分析:(1)结合图形,由已知先证明CGHF为正方形,求出DF的长,进而求出DH.
(2)两个面积相等转换为另外两个相等即可,即△BCF与△DCE面积相等.
(3)根据平行线的关系容易证明
=
,代入数值求解即可.
(2)两个面积相等转换为另外两个相等即可,即△BCF与△DCE面积相等.
(3)根据平行线的关系容易证明
| BE |
| BC-BE |
| CD-BE |
| CD |
解答: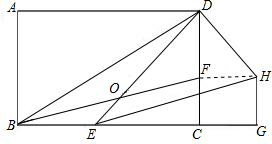 解:(1)连接FH,
解:(1)连接FH,
∵△EGH≌△BCF,
∴∠DCB=∠G=90°,FC=GH,
∴FC∥GH,
∴四边形FCGH是平行四边形,
∴四边形FCGH是矩形,
∴两动点E、F分别从顶点B、C同时开始以相同速度在边BC、CD上运动
∴BE=CF=1
∵矩形ABCD中,边长AB=3,tan∠ABD=
∴BC=4
∴EC=3
∵EG=BC
∴CG=1
∴CG=CF,
∴四边形CGHF为正方形
∴DF=2 FH=1
∴DH=
;
(2)要使△BOE与△DOF的面积相等,由图看出只要△BCF与△DCE面积相等即可
∵SBCF=
×BC×CF,SDCE=
×CE×CD,
∵由(1)可知,CF=BE,△EGH在运动过程中始终保持△EGH≌△BCF,
∴CF=BE=4-CE不会发生变化,
∴BC×BE=(4-BE)×CD
∴代入数值得BE=
;
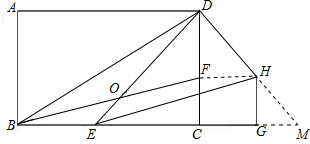
(3)由题意知DM=DE
∴CD为EM的垂直平分线
由(1)中知FH∥BC
∴
=
∵FH=BE=FC CE=BC-BE
∴
=
代入数值得
=
,
解得BE=5-
.
 解:(1)连接FH,
解:(1)连接FH,∵△EGH≌△BCF,
∴∠DCB=∠G=90°,FC=GH,
∴FC∥GH,
∴四边形FCGH是平行四边形,
∴四边形FCGH是矩形,
∴两动点E、F分别从顶点B、C同时开始以相同速度在边BC、CD上运动
∴BE=CF=1
∵矩形ABCD中,边长AB=3,tan∠ABD=
| 4 |
| 3 |
∴BC=4
∴EC=3
∵EG=BC
∴CG=1
∴CG=CF,
∴四边形CGHF为正方形
∴DF=2 FH=1
∴DH=
| 5 |
(2)要使△BOE与△DOF的面积相等,由图看出只要△BCF与△DCE面积相等即可
∵SBCF=
| 1 |
| 2 |
| 1 |
| 2 |
∵由(1)可知,CF=BE,△EGH在运动过程中始终保持△EGH≌△BCF,
∴CF=BE=4-CE不会发生变化,
∴BC×BE=(4-BE)×CD
∴代入数值得BE=
| 12 |
| 7 |

(3)由题意知DM=DE
∴CD为EM的垂直平分线
由(1)中知FH∥BC
∴
| FH |
| CM |
| DF |
| DC |
∵FH=BE=FC CE=BC-BE
∴
| BE |
| BC-BE |
| CD-BE |
| CD |
代入数值得
| BE |
| 4-BE |
| 3-BE |
| 3 |
解得BE=5-
| 13 |
点评:注意题中的隐含条件的发掘,综合运用所学知识便于求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
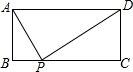 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
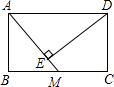 如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为
如图,矩形ABCD中,AB=6,BC=8,M是BC的中点,DE⊥AM,E是垂足,则△ABM的面积为 7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE=
7、如图,矩形ABCD中,AE⊥BD,垂足为E,∠DAE=2∠BAE,则∠CAE= (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为 (2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.
(2002•西藏)已知:如图,矩形ABCD中,E、F是AB边上两点,且AF=BE,连结DE、CF得到梯形EFCD.