题目内容
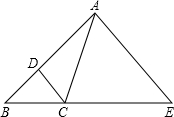 如图,CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠ACE=80°.求∠CAE的度数.
如图,CD平分∠ACB,AE∥DC交BC的延长线于点E,若∠ACE=80°.求∠CAE的度数.
分析:根据邻补角的定义求得∠ACB=100°;然后利用角平分线的定义求得∠DCA=100°×
=50°;最后由平行线的性质和等量代换求得∠CAE的度数.
| 1 |
| 2 |
解答:解:∵∠ACE=80°(已知),
∴∠ACB=100°(邻补角的定义),
又∵CD平分∠ACB(已知),
∴∠DCA=100°×
=50°;
∵AE∥DC(已知),
∴∠CAE=∠DCA=50°(两直线平行,内错角相等).
∴∠ACB=100°(邻补角的定义),
又∵CD平分∠ACB(已知),
∴∠DCA=100°×
| 1 |
| 2 |
∵AE∥DC(已知),
∴∠CAE=∠DCA=50°(两直线平行,内错角相等).
点评:此题结合了平行线的性质和角平分线的定义,是一道较为简单的题目.利用邻补角的定义求得∠ACB=100°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 19、如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.(写出推理过程)
19、如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.(写出推理过程) 22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB. 12、如图:CD平分∠ACB,DE∥AC且∠1=30°,则∠2=
12、如图:CD平分∠ACB,DE∥AC且∠1=30°,则∠2= 如图,CD平分∠ACB,DE∥AC,EF∥CD,求证:EF平分∠BED.
如图,CD平分∠ACB,DE∥AC,EF∥CD,求证:EF平分∠BED. 如图,CD平分∠ACB,DE∥AC,EF∥CD,EF平分∠DEB吗?请说明你的理由.
如图,CD平分∠ACB,DE∥AC,EF∥CD,EF平分∠DEB吗?请说明你的理由.