题目内容
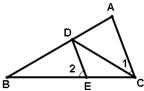 19、如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.(写出推理过程)
19、如图,CD平分∠ACB,DE∥AC,且∠1=35°,求∠2的度数.(写出推理过程)分析:由于CD平分∠ACB,所以∠1=∠DCE,又因为DE∥AC,根据平行线的性质定理,所以∠1=∠CDE,根据三角形的外角的性质,∠2=∠ECD+∠CDE,所以∠2=70°.
解答:解:∵CD平分∠ACB,
∴∠1=∠DCE,
又∵DE∥AC,
∴∠1=∠CDE,
∵∠1=35°,
∴∠CDE=∠DCE=35°;
∵∠2=∠ECD+∠CDE,
∴∠2=35°+35°=70°.
∴∠1=∠DCE,
又∵DE∥AC,
∴∠1=∠CDE,
∵∠1=35°,
∴∠CDE=∠DCE=35°;
∵∠2=∠ECD+∠CDE,
∴∠2=35°+35°=70°.
点评:本题结合角的平分线的定义,考查了平行线的性质.角平分线的性质和平行线的性质都是证明角相等的重要依据,题目往往将二者结合起来考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
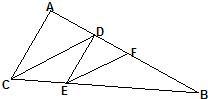 22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.
22、已知,如图,CD平分∠ACB,AC∥DE,CD∥EF,求证:EF平分∠DEB.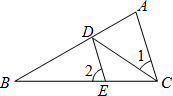 12、如图:CD平分∠ACB,DE∥AC且∠1=30°,则∠2=
12、如图:CD平分∠ACB,DE∥AC且∠1=30°,则∠2=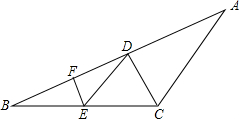 如图,CD平分∠ACB,DE∥AC,EF∥CD,求证:EF平分∠BED.
如图,CD平分∠ACB,DE∥AC,EF∥CD,求证:EF平分∠BED.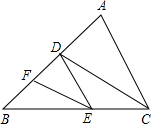 如图,CD平分∠ACB,DE∥AC,EF∥CD,EF平分∠DEB吗?请说明你的理由.
如图,CD平分∠ACB,DE∥AC,EF∥CD,EF平分∠DEB吗?请说明你的理由.