题目内容
【题目】如图,在Rt△ABC中,∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.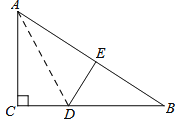
(1)问:△BDE与△BAC相似吗?
(2)已知AC=6,BC=8,求线段AD的长度.
【答案】
(1)
解答:相似.理由如下:
∵∠C= ![]() ,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,
,△ACD沿AD折叠,使得点C落在斜边AB上的点E处,
∴∠C=∠AED= ![]() ,
,
∴∠DEB=∠C= ![]() ,
,
∵∠B=∠B,
∴△BDE∽△BAC;
(2)
解答:由勾股定理,得
AB= ![]() =10.
=10.
由折叠的性质知,AE=AC=6,DE=CD,∠AED=∠C= ![]() .
.
∴BE=AB-AE=10-6=4,
在Rt△BDE中,由勾股定理得,
![]() ,
,
即 ![]() ,
,
解得:CD=3,
在Rt△ACD中,由勾股定理得 ![]()
即 ![]() ,
,
解得:AD=3
【解析】根据折叠的性质得出∠C=∠AED= ![]() ,利用∠DEB=∠C , ∠B=∠B证明三角形相似;先由勾股定理求出AB的长,再由折叠的性质知DE=CD , AE=AC , BE=AB-AE , 在Rt△BDE中运用勾股定理求出DE , 即CD , 最后在Rt△ACD中运用勾股定理得出AD .
,利用∠DEB=∠C , ∠B=∠B证明三角形相似;先由勾股定理求出AB的长,再由折叠的性质知DE=CD , AE=AC , BE=AB-AE , 在Rt△BDE中运用勾股定理求出DE , 即CD , 最后在Rt△ACD中运用勾股定理得出AD .
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目