题目内容
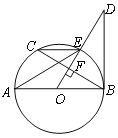
【题目】如图所示，已知
，
分别是
的高和中线，
，
，
，
，试求：
(1)的长；
(2)
和
的周长的差.
【答案】(1)
长为
;(2)周长差
.
【解析】
（1）利用直角三角形的面积法求线段AD的长度；
（2）由于AE是中线，那么BE=CE，再表示△ACE的周长和△ABE的周长，化简可得△ACE的周长-△ABE的周长=AC-AB，即可求解．
解：（1）∵∠BAC=90°，AD是边BC上的高，
∴S△ACB=
ABAC=BCAD，
∵
，
，
，
∴AD=8×15÷17=
（cm），
即AD的长度为cm；
（2）∵AE为BC边上的中线，
∴BE=CE，
∴△ACE的周长-△ABE的周长=AC+AE+CE-（AB+BE+AE）=AC-AB=15-8=7（cm），
即△ACE和△ABE的周长的差是7cm．
【题目】小南发现操场中有一个不规则的封闭图形ABC．为了知道它的面积，他在封闭图形内画出了一个半径为1米的圆，在不远处向圈内掷石子，若石子落在图形ABC以外，则重掷．记录如下：
石子落在圆内（含圆上）的次数 | 14 | 43 | 93 | 150 |
石子落在阴影内的次数 | 23 | 91 | 186 | 300 |
根据以上的数据，小南得到了封闭图形ABC的面积．
请根据以上信息，回答以下问题：
（1）求石子落在圆内（含圆上）的频率；
（2）估计封闭图形ABC的面积．
【题目】（1）某校招聘教师一名，现有甲、乙、丙三人通过专业知识、讲课、答辩三项测试，他们各自的成绩如下表所示：
应聘者 | 专业知识 | 讲课 | 答辩 |
甲 | 70 | 85 | 80 |
乙 | 90 | 85 | 75 |
丙 | 80 | 90 | 85 |
按照招聘简章要求，对专业知识、讲课、答辩三项赋权5：4：1．请计算三名应聘者的平均成绩，从成绩看，应该录取谁？
（2）我市举行了某学科实验操作考试，有A、B、C、D四个实验，规定每位学生只参加其中一个实验的考试，并由学生自己抽签决定具体的考试实验．小王，小张，小厉都参加了本次考试．
①小厉参加实验D考试的概率是 ；
②用列表或画树状图的方法求小王、小张抽到同一个实验的概率．
