题目内容
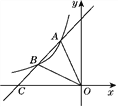
【题目】如图,直线y=k1x+b与反比例函数y=![]() (x<0)的图象相交于点A,B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(x<0)的图象相交于点A,B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.
(1)试确定反比例函数的表达式;
(2)求△AOC的面积.
【答案】(1)y=-![]() (2)12
(2)12
【解析】试题分析:(1)点A(-2,4)在反比例函数y=![]() (x<0)上,将A点代入即可求出反比例函数的表达式;
(x<0)上,将A点代入即可求出反比例函数的表达式;
(2)根据点B在反比例函数上且B的横坐标为-4,结合反比例函数的表达式即可求出B的坐标,将A和B的坐标带入一次函数的表达式y=k1x+b,即可求出一次函数的表达式;因为点C在x轴上即纵坐标为0,且点C在一次函数上进而可求出点C的坐标;观察图形可知,点A的纵坐标的绝对值即为三角形ACO的高,点C的横坐标的绝对值为三角形ACO的底边,进而根据三角形的面积公式即可求解.
试题解析:∵点A(-2,4)在反比例函数y=![]() 的图象上,
的图象上,
∴4=![]() ,
,
∴k2=-8.
∴反比例函数的表达式为y=-![]() .
.
(2)∵B点的横坐标为-4,
∴其纵坐标为2,
∴B(-4,2).
∵点A(-2,4),B(-4,2)在直线y=k1x+b上,
∴![]() ,解得
,解得![]()
∴直线AB对应的函数表达式为y=x+6,
∴直线AB与x轴的交点为C(-6,0).
∴S△AOC=![]() ×6×4=12.
×6×4=12.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目