题目内容
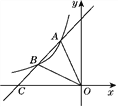
【题目】如图,△ABC的高AD、BF相交于点E,AD=BD,BC=6cm,DC=2cm,
(1)求证:△BDE≌△ADC;(2)求AE的长.

【答案】证明见解析;(2)2cm.
【解析】试题分析:
(1)由已知条件易证∠DBE和∠DAC都与∠C互余,由此可得∠DBE=∠DAC,从而可用“ASA”证得△BDE≌△ADC.
(2)由(1)中△BDE≌△ADC可得DE=DC=2cm,结合AD=BD=BC-DC=4cm可解得:AE=AD-DE=4-2=2cm.
试题解析:
(1)∵AD、BF是△ABC的高,
∴∠BDE=∠ADC=∠BFC=90°,
∴∠EBD+∠C=90°,∠DAC+∠C=90°,
∴∠EBD=∠DAC,
在△BDE和△ADC中:  ,
,
∴△BDE≌△ADC.
(2)∵△BDE≌△ADC,
∴DE=DC=2,
又∵AD=BD=BC-DC=4,
∴AE=AD-DE=4-2=2(cm).

练习册系列答案
相关题目