题目内容
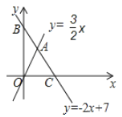
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
(1)求![]() 点坐标;
点坐标;
(2)如果在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 是以
是以![]() 为底边的等腰三角形,求
为底边的等腰三角形,求![]() 点坐标;
点坐标;
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于6?若存在,请求出
的面积等于6?若存在,请求出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 点坐标是
点坐标是![]() ;(3)存在;点
;(3)存在;点![]() 的坐标是
的坐标是![]() 或
或![]()
【解析】
(1)联立方程组即可解答;
(2)设![]() 点坐标是
点坐标是![]() ,表达出OP=PA在解方程即可;
,表达出OP=PA在解方程即可;
(3)对Q点分类讨论,①当点![]() 在线段
在线段![]() 上;②当点
上;②当点![]() 在
在![]() 的延长线上,表达出
的延长线上,表达出![]() 的面积即可求解.
的面积即可求解.
解:(1)解方程组: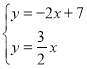 ,得
,得![]()
∴![]() ;
;
(2)设![]() 点坐标是
点坐标是![]() ,
,
∵![]() 是以
是以![]() 为底边的等腰三角形,
为底边的等腰三角形,
∴![]() ,
,
∴![]()
解得![]()
∴![]() 点坐标是
点坐标是![]()
(3)存在;
由直线![]() 可知
可知![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]() 点有两个位置:
点有两个位置:![]() 在线段
在线段![]() 上和
上和![]() 的延长线上
的延长线上
设点![]() 的坐标是
的坐标是![]() ,
,
①当点![]() 在线段
在线段![]() 上:作
上:作![]() 轴于点
轴于点![]() ,如图①,则
,如图①,则![]() ,
,
∴![]()
∴![]() ,即
,即![]()
∴![]()
把![]() 代人了
代人了![]() ,得7
,得7![]() ,
,
∵![]() 的坐标是
的坐标是![]()
②当点![]() 在
在![]() 的延长线上:作
的延长线上:作![]() 轴于点
轴于点![]() ,如图②,则
,如图②,则![]() ,
,
∴![]()
∴![]() ,即
,即![]()
∴![]()
把![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() 的坐标是
的坐标是![]()
综上所述:点![]() 的坐标是
的坐标是![]() 或
或![]()

练习册系列答案
相关题目
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?