题目内容
【题目】如图，在△ABC中，已知AB=BC，∠B=120°，AB的垂直平分线交AC于点D，若AC=6，求AD的长． 
【答案】解：连接BD，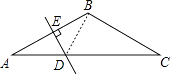 
∵AB=BC，∠ABC=120°，
∴∠A=∠C= 
（180°﹣∠ABC）=30°，
∴DC=2BD，
∵AB的垂直平分线是DE，
∴AD=BD，
∴DC=2AD，
∵AC=6，
∴AD= ×6=2
【解析】连接BD，根据三角形的内角和定理和等腰三角形性质推出∠C=30°，根据含30°角的直角三角形性质得出DC=2BD，根据线段垂直平分线的性质推出AD=BD，即可求出答案．
【考点精析】通过灵活运用线段垂直平分线的性质和含30度角的直角三角形，掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线；线段垂直平分线的性质定理：线段垂直平分线上的点和这条线段两个端点的距离相等；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半即可以解答此题．
【题目】某品牌汽车生产厂为了占领市场提高销售量，对经销商采取销售奖励活动，在2014年10月前奖励办法以下表计算奖励金额，2014年10月后以新奖励办法执行．某经销商在新奖励办法出台前一个月共售出某品牌汽车的A型和B型共413台，新奖励办法出台后的第一个月售出这两种型号的汽车共510台，其中A型和B型汽车的销售量分别比新奖励办法出台前一个月增长25％和20％．2014年10月前奖励办法：
销售量（x台） | 每台奖励金额（元） |
0＜x≤ 100 | 200 |
100＜x≤300 | 500 |
x＞300 | 1000 |
（1）在新办法出台前一个月，该经销商共获得奖励金额多少元？
（2）在新办法出台前一个月，该经销商销售的A型和B型汽车分别为多少台？
（3）若A型汽车每台售价为10万元，B型汽车每台售价为12万元．新奖励办法是：每销售一台A型汽车按每台汽车售价的 
给予奖励，每销售一台B型汽车按每台汽车售价的 
给予奖励．新奖励办法出台后的第二个月，A型汽车的销售量比出台后的第一个月增加了 
；而B型汽车受到某问题零件召回的影响，销售量比出台后的第一个月减少了 
，新奖励办法出台后的第二个月该经销商共获得的奖励金额355680元，求 
的值．
