题目内容
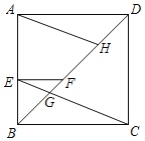
【题目】如图,正方形ABCD中,E为AB边上一点,过点E作EF⊥AB交对角线BD于点F.连接EC交BD于点G.取DF的中点H,并连接AH.若AH=![]() ,EG=
,EG=![]() ,则四边形AEFH的面积为___.
,则四边形AEFH的面积为___.
【答案】![]()
【解析】
如图,连接HE,HC,作HM⊥AB于M,延长MH交CD于N.证明△ADH≌△CDH,得到AH=CH=![]() ,证明四边形AMND是矩形,得到AM=DN,进而得到EM=HN,
,证明四边形AMND是矩形,得到AM=DN,进而得到EM=HN,
证明Rt△HME≌Rt△CNH,得到∠MHE=∠HCN,设EF=BE=4a,则BC=AB=10a,AE=6a,AM=ME=3a,根据EF∥HM,得到![]() =
=![]() ,进而得到HM=7a,进而求出S四边形AEFH
,进而得到HM=7a,进而求出S四边形AEFH
,在Rt△BEC中,根据勾股定理得到16a2+100a2=4,即可求出![]() 的值,进而得到四边形AEFH的面积.
的值,进而得到四边形AEFH的面积.
如图,连接HE,HC,作HM⊥AB于M,延长MH交CD于N.
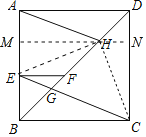
∵四边形ABCD是正方形,
∴DA=DC,∠ADH=∠CDH=45°,
∵DH=DH,
∴△ADH≌△CDH(SAS),
∴AH=CH=![]() ,
,
∵EF⊥AB,HM⊥AB,DA⊥AB,
∴EF∥HM∥AD,
∵HF=HD,
∴AM=EM,
∴HA=HE=HC,
∵∠AMN=∠DAM=∠ADN=90°,
∴四边形AMND是矩形,
∴AM=DN,
由题可证得DN=HN,
又∵AM=EM,
∴EM=HN,
∴Rt△HME≌Rt△CNH(HL),
∴∠MHE=∠HCN,
∵∠HCN+∠CHN=90°,
∴∠MHE+∠CHN=90°,
∴∠EHC=90°,
∴EC=![]() HE=2,
HE=2,
∵EG=![]() ,
,
∴GC=2–![]() =
=![]() ,
,
∵EF∥BC,
∴![]() =
=![]() =
=![]() ,
,
设EF=BE=4a,则BC=AB=10a,AE=6a,AM=ME=3a,
∵EF∥HM,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴HM=7a,
∴S四边形AEFH=S△AMH+S梯形EFHM=![]() ×3a×7a+
×3a×7a+![]() (4a+7a)×3a=27a2,
(4a+7a)×3a=27a2,
在Rt△BEC中,
∵BE2+BC2=EC2,
∴16a2+100a2=4,
∴a2=![]() ,
,
∴S四边形AEFH=![]() .
.
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案