Question

（2013•松江区二模）三角形的三条高或其延长线相交于一点，这点称为三角形的垂心．边长为2的等边三角形的垂心到这个三角形各顶点之间的距离之和为

2

3

．

Answer 1

分析：根据△ABC是等边三角形，边长为2，得出OA=OB=OC，AF=CE=1，根据勾股定理求出AE的值，根据Rt△AOF∽Rt△ACE，求出AO的值，从而求出答案．

解答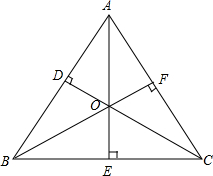：解：如图：
∵△ABC是等边三角形，
∴OA=OB=OC，
∵AB=AC=BC=2，
∴AF=CE=1，
∴AE=

AC2-CE2

=

22-12

=

3

，
∵Rt△AOF∽Rt△ACE，
∴

AO

AC

=

AF

AE

，
∴

AO

2

=

1

3

，
∴AO=

2

3

=

2 3

3

，
∴OA+OB+OC=3×

2 3

3

=2

3

．
故答案为：2

3

．

点评：此题考查了等边三角形的性质，用到的知识点是等边三角形的性质，勾股定理，相似三角形的判断及性质，解题的关键是根据题意画出图形，再根据垂心的定义求解．