题目内容
一个圆锥的侧面展开图是一个半圆，高为3
，则圆锥的表面积为________．
27π
分析：设出圆锥的母线长和底面半径，用两种方式表示出全面积，即可求得圆锥底面半径和母线长的关系，加上高利用勾股定理即可求得圆锥的母线长和底面半径，那么圆锥的侧面积=底面周长×母线长÷2．
解答：设底面半径为r，母线长为R，则底面周长=2πr，侧面积=
×2πrR=πR2，
∴R=2r，
由勾股定理得，R2=（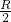
）2+（3）2，
∴R=6，r=3，
∴圆锥的表面积=圆锥的侧面积+底面积=18π+9π=27π．
故答案为27π．
点评：本题考查了圆锥的计算，利用了勾股定理，圆的面积公式，圆的周长公式和扇形面积公式求解．
分析：设出圆锥的母线长和底面半径，用两种方式表示出全面积，即可求得圆锥底面半径和母线长的关系，加上高利用勾股定理即可求得圆锥的母线长和底面半径，那么圆锥的侧面积=底面周长×母线长÷2．
解答：设底面半径为r，母线长为R，则底面周长=2πr，侧面积=
×2πrR=πR2，∴R=2r，
由勾股定理得，R2=（
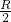）2+（3）2，∴R=6，r=3，
∴圆锥的表面积=圆锥的侧面积+底面积=18π+9π=27π．
故答案为27π．
点评：本题考查了圆锥的计算，利用了勾股定理，圆的面积公式，圆的周长公式和扇形面积公式求解．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
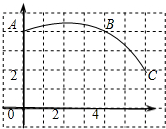如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
（2013•本溪二模）一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是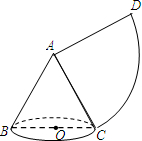
如图，一个圆锥的侧面展开图是90°的扇形．
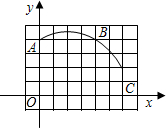如图，在单位长度为1的正方形网格中建立平面直角坐标系，一段圆弧经过网格的交点为A、B、C．