题目内容
如图，一个圆锥的侧面展开图是90°的扇形．（1）求圆锥的母线长l与底面半径r之比；
（2）若底面半径r=2，求圆锥的高及侧面积（结果保留π）．
分析：（1）利用底面圆的周长等于扇形的弧长进而得出即可；
（2）首先求出l的值，进而利用勾股定理求出h和圆锥的侧面积．
（2）首先求出l的值，进而利用勾股定理求出h和圆锥的侧面积．
解答：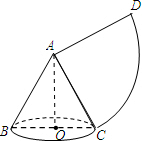
解：（1）由已知得：
2πr=
，
∴
=4．
（2）设此圆锥的高为h，在Rt△AOC中，
∵
=4，r=2
∴l=8，
h=
=
=2
，
∴圆锥的侧面积为πrl=π×2×8=16π．
解：（1）由已知得：2πr=
| 90πl |
| 180 |
∴
| l |
| r |
（2）设此圆锥的高为h，在Rt△AOC中，
∵
| l |
| r |
∴l=8，
h=
| l2-r2 |
| 82-22 |
| 15 |
∴圆锥的侧面积为πrl=π×2×8=16π．
点评：此题主要考查了圆锥的计算，根据已知得出l与r的关系是解题关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
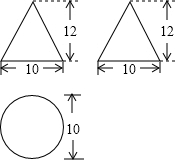如图是一个圆锥的三视图，求它的母线长和侧面积．（结果保留π）
如图，一个圆锥的高为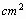
(图示两条线段的长都是4cm)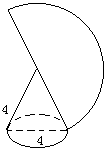
如图，一个圆锥的侧面展开图是90°的扇形．