题目内容
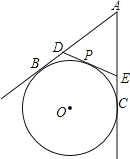
【题目】已知,如图,AB、AC是⊙O得切线,B、C是切点,过![]() 上的任意一点P作⊙O的切线与AB、AC分别交于点D、E
上的任意一点P作⊙O的切线与AB、AC分别交于点D、E
(1)连接OD和OE,若∠A=50°,求∠DOE的度数.
(2)若AB=7,求△ADE的周长.
【答案】(1)65°;(2)14.
【解析】
试题分析:(1)连接OB,OC,OD,OP,OE,由题意可知OB⊥AB,OC⊥AC,OP⊥DE,DB=DP,EP=EC,AB=AC,由∠A=50°,可算出∠BOC=360°﹣90°﹣90°﹣50°=130°,又由OD平分∠BOP,OE平分∠POC,可得∠DOE=∠DOP+∠EOP=![]() (∠BOP+∠POC)=
(∠BOP+∠POC)=![]() ∠BOC.于是得出结论.(2) 因为DB=DP,EP=EC,AB=AC,所以△ADE的周长可转化成AB加AC的长,于是得出结论.
∠BOC.于是得出结论.(2) 因为DB=DP,EP=EC,AB=AC,所以△ADE的周长可转化成AB加AC的长,于是得出结论.
试题解析:(1)如图:连接OB,OC,OD,OP,OE,
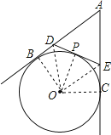 ,∵AB,AC,DE分别与⊙O相切,OB,OC,OP是⊙O的半径,∴OB⊥AB,OC⊥AC,OP⊥DE,DB=DP,EP=EC,AB=AC,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=360°﹣90°﹣90°﹣50°=130°,∵OB⊥AB,OP⊥DE,DB=DP,∴OD平分∠BOP,同理得:OE平分∠POC,∴∠DOE=∠DOP+∠EOP=
,∵AB,AC,DE分别与⊙O相切,OB,OC,OP是⊙O的半径,∴OB⊥AB,OC⊥AC,OP⊥DE,DB=DP,EP=EC,AB=AC,∴∠OBA=∠OCA=90°,∵∠A=50°,∴∠BOC=360°﹣90°﹣90°﹣50°=130°,∵OB⊥AB,OP⊥DE,DB=DP,∴OD平分∠BOP,同理得:OE平分∠POC,∴∠DOE=∠DOP+∠EOP=![]() (∠BOP+∠POC)=
(∠BOP+∠POC)=![]() ∠BOC=65°,(2)由题意可知DB=DP,EP=EC,AB=AC,∴△ADE的周长=AD+DE+AE=AD+DP+EP+AE=AD+BD+AE+EC=AB+AC=2AB=14.
∠BOC=65°,(2)由题意可知DB=DP,EP=EC,AB=AC,∴△ADE的周长=AD+DE+AE=AD+DP+EP+AE=AD+BD+AE+EC=AB+AC=2AB=14.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目