题目内容
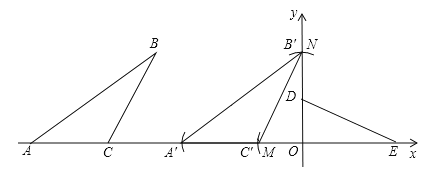
【题目】在平面直角坐标系xOy中,如图,已知Rt△DOE,∠DOE=90°,OD=3,点D在y轴上,点E在x轴上,在△ABC中,点A,C在x轴上,AC=5.∠ACB+∠ODE=180°,∠ABC=∠OED,BC=DE.按下列要求画图(保留作图痕迹):
(1)将△ODE绕O点按逆时针方向旋转90°得到△OMN(其中点D的对应点为点M,点E的对应点为点N),画出△OMN;
(2)将△ABC沿x轴向右平移得到△A′B′C′(其中点A,B,C的对应点分别为点A′,B′,C′),使得B′C′与(1)中的△OMN的边NM重合;
(3)求OE的长.
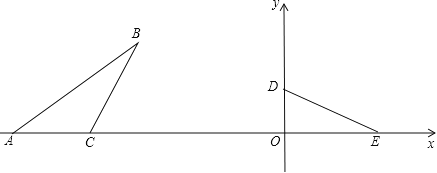
【答案】(1)作图见解析;(2)作图见解析;(3)6.
【解析】
试题(1)以点O为圆心,以OE为半径画弧,与y轴正半轴相交于点M,以OD为半径画弧,与x轴负半轴相交于点N,连接MN即可.
(2)以M为圆心,以AC长为半径画弧与x轴负半轴相交于点A′,B′与N重合,C′与M重合,然后顺次连接即可.
(3)设OE=x,则ON=x,作MF⊥A′B′于点F,判断出B′C′平分∠A′B′O,再根据角平分线上的点到角的两边距离相等和角平分线的对称性可得B′F=B′O=OE=x,F C′="O" C′=OD=3,利用勾股定理列式求出A′F,然后表示出A′B′、A′O,在Rt△A′B′O中,利用勾股定理列出方程求解即可.
试题解析:解:(1)△OMN如图所示.
(2)△A′B′C′如图所示.
(3)设OE=x,则ON=x,如答图,过点M作MF⊥A′B′于点F,
由作图可知:B′C′平分∠A′B′O,且C′O⊥O B′,
∴B′F=B′O=OE=x,F C′="O" C′=OD=3,
∵A′C′=AC=5,∴![]() .∴A′B′=x+4,A′O=5+3=8.
.∴A′B′=x+4,A′O=5+3=8.
在Rt△A′B′O中,![]() ,解得x=6.
,解得x=6.
∴OE=6.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案