Question

【题目】新知认识：在△ABC中，∠A，∠B，∠C所对的边分别用a，b，c表示，如果一个三角形的一个内角等于另一个内角的2倍，我们称这样的三角形为“倍角三角形”．

（1）特殊验证：如图1，在△ABC中，若a＝，b＝1，c＝2，求证：△ABC为倍角三角形；

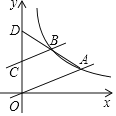
（2）模型探究：如图2，对于任意的倍角三角形，若∠A＝2∠B，求证：a2＝b（b+c）

Answer 1

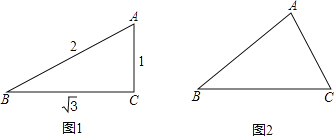
【答案】（1）证明见解析；（2）证明见解析

【解析】

)利用勾股定理的逆定理求得为直角三角形，由锐角三角函数求得三角形的三个内角，根据“倍角三角形”的定义进行证明即可；
如图2，延长BA至D，使，通过证明∽，可得，结合等腰三角形的等角对等边的性质，可得结论．

证明：（1）如图1，，，．
，
，
，
∴∠B＝30°，

∴

∴∠A＝2∠B．

∴△ABC为倍角三角形；

（2）如图2，延长BA至D，使AD＝AC，

∴∠D＝∠ACD，

∵∠BAC＝∠D+∠ACD＝2∠D，且∠BAC＝2∠B，

∴∠B＝∠D＝∠ACD，

∴BC＝CD＝a，AD＝AC＝b，

∴BD＝AB+AD＝b+c，

∵∠D＝∠D，∠B＝∠ACD，

∴△ACD∽△CBD．

，
，
∴.