题目内容
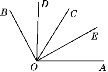
【题目】如图,OD平分∠BOC,OE平分∠AOC,∠BOC=60°,∠AOC=58°.
(1)求出∠AOB及其补角的度数;
(2)①请求出∠DOC和∠AOE的度数;
②判断∠DOE与∠AOB是否互补,并说明理由.
【答案】(1)118°;62°(2)①29°②不互补
【解析】
(1)由∠AOB=∠BOC+∠AOC可求出∠AOB的度数,进而求出其补角的度数.
(2)①由OD和OE是∠BOC和∠AOC的平分线可求出∠DOC和∠AOE的度数.
②由∠DOE=∠DOC+∠COE可知∠DOE的度数,计算∠AOB与∠DOE的和即可判断∠AOB与∠DOE是否为补角.
(1)∠AOB=∠BOC+∠AOC=60°+58°=118°,
其补角为180°-∠AOB=180°-118°=62°.
(2)①因为OD平分∠BOC,OE平分∠AOC,
所以∠DOC=∠BOD=![]() ∠BOC=
∠BOC=![]() ×60°=30°,∠AOE=∠COE=
×60°=30°,∠AOE=∠COE=![]() ∠AOC=
∠AOC=![]() ×58°=29°.
×58°=29°.
②∠DOE与∠AOB不互补.
理由:因为∠DOC=30°,∠COE=29°,
所以∠DOE=∠DOC+∠COE=59°.
所以∠DOE+∠AOB=59°+118°=177°,![]()
故∠DOE与∠AOB不互补.

练习册系列答案
相关题目
【题目】某校七年级(1)班体育委员统计了全班同学60秒跳绳次数,并列出了下面的不完整频数分布表和不完整的频数分布直方图.根据图表中的信息解答问题
组别 | 跳绳次数 | 频数 |
A | 60≤x<80 | 2 |
B | 80≤x<100 | 6 |
C | 100≤x<120 | 18 |
D | 120≤x<140 | 12 |
E | 140≤x<160 | a |
F | 160≤x<180 | 3 |
G | 180≤x<200 | 1 |
合计 | 50 | |
(1)求a的值;
(2)求跳绳次数x在120≤x<180范围内的学生的人数;
(3)补全频数分布直方图,并指出组距与组数分别是多少?