题目内容
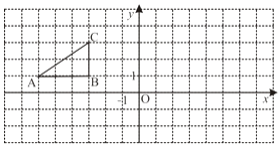
【题目】如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线![]() 与x轴、y轴分别交于点D、E,交OB于点F.
与x轴、y轴分别交于点D、E,交OB于点F.
(1)写出图中的全等三角形及理由;
(2)求OF的长.

【答案】(1)△AOB≌△OED,理由见解析;(2)OF=![]() .
.
【解析】
(1)先求出D、E两点的坐标,进而可得出OD、OE的长,再由B点坐标可得出OA,AB的长,由此可得出结论;
(2)先根据全等三角形的性质得出∠AOB=∠OED,再由余角的定义得出OF⊥ED,由勾股定理得出ED的长,再由三角形的面积公式即可得出结论.
(1)△AOB≌△OED.
理由:∵y=-![]() x+4与x轴、y轴分别交于点D、E,
x+4与x轴、y轴分别交于点D、E,
∴D(3,0),E(0,4),
∴OD=3,OE=4.∵B(4,3),∴OA=4,AB=3.
在△AOB与△OED中,
∵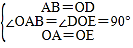 ,
,
∴△AOB≌△OED(SAS);
(2)∵△AOB≌△OED,
∴∠AOB=∠OED.
∵∠AOB+∠EOF=90°,
∴∠OED+∠EOF=90°,
∴∠OFE=90°,
∴OF⊥ED.
在Rt△ODE中,ED=![]() =
=![]() =5
=5
∵S△ODE=![]() ODOE=
ODOE=![]() DEOF=6,
DEOF=6,
∴OF=![]() .
.

练习册系列答案
相关题目