题目内容
推理填空:
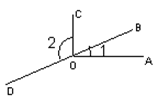
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。理由如下:

∵ ∠1 =∠2(已知),且∠1 =∠4( ),
∴ ∠2 =∠4(等量代换),
∴ CE∥BF( ).
∴ ∠ =∠3( ).
又∵ ∠B =∠C(已知),
∴ ∠3 =∠B(等量代换),
∴ AB∥CD( ).
如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。理由如下:

∵ ∠1 =∠2(已知),且∠1 =∠4( ),
∴ ∠2 =∠4(等量代换),
∴ CE∥BF( ).
∴ ∠ =∠3( ).
又∵ ∠B =∠C(已知),
∴ ∠3 =∠B(等量代换),
∴ AB∥CD( ).
对顶角相等
同位角相等,两直线平行
∠C
两直线平行,同位角相等
内错角相等,两直线平行
同位角相等,两直线平行
∠C
两直线平行,同位角相等
内错角相等,两直线平行
试题分析:∵ ∠1 =∠2(已知),且∠1 =∠4(对顶角相等),
∴ ∠2 =∠4(等量代换),
∴ CE∥BF(同位角相等,两直线平行).
∴ ∠C=∠3(两直线平行,同位角相等).
又∵ ∠B =∠C(已知),
∴ ∠3 =∠B(等量代换),
∴ AB∥CD(内错角相等,两直线平行)
点评:本题难度较低,主要考查学生对平行线判定与性质知识点的掌握。根据已知步骤,判断所用性质定理即可。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目




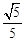


 点出发,要到距离
点出发,要到距离
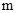 的
的 地去,先沿北偏东
地去,先沿北偏东 方向到达
方向到达 地,然后再沿北偏西
地,然后再沿北偏西 方向走了
方向走了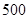

 方向上
方向上 方向上
方向上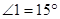 ,
,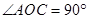 ,点B、O、D在同一直线上,则
,点B、O、D在同一直线上,则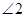 的度数为 .
的度数为 .