题目内容
 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.(1)DE与半圆O相切吗?若相切,请给出证明;若不相切,说明理由;
(2)如果AD,AB的长是方程x2-10x+24=0的两个根,试求直角边BC的长;
(3)试在(1)(2)的基础上,提出一个有价值的问题(不必解答).
分析:(1)连接OD,BD,根据图形中角与角之间的关系易得∠EDO=90°,故OD⊥DE,DE与半圆O相切;
(2)求解方程可得AD,AB的长,同时易得Rt△ABD∽Rt△ACB,即AB2=AD•AC,根据勾股定理可得BC的长;
(3)根据题意,提出问题即可,如求四边形ABED的面积,符合题意即可.
(2)求解方程可得AD,AB的长,同时易得Rt△ABD∽Rt△ACB,即AB2=AD•AC,根据勾股定理可得BC的长;
(3)根据题意,提出问题即可,如求四边形ABED的面积,符合题意即可.
解答: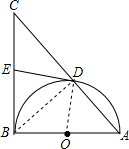 解:(1)DE与半圆O相切.
解:(1)DE与半圆O相切.
证明:连接OD,BD,
∵AB是半圆O的直径,
∴∠BDA=∠BDC=90°.
∵在Rt△BDC中,E是BC边上的中点,
∴DE=BE=
BC,得∠EBD=∠BDE.
∵OB=OD,
∴∠OBD=∠ODB.
又∵∠ABC=∠OBD+∠EBD=90°,
∴∠ODB+∠EDB=90°,故DE与半圆O相切.
(2)∵BD⊥AC,
∴Rt△ABD∽Rt△ACB.
∴
=
.
即AB2=AD•AC.
∴AC=
.
∵AD,AB的长是方程x2-10x+24=0的两个根,
∴解方程得x1=4,x2=6.
∵AD<AB,
∴AD=4,AB=6.
∴AC=
=
=9.
又∵在Rt△ABC中,AB=6,AC=9,
∴BC=
=
=3
.
(3)问题1:求四边形ABED的面积;
问题2:求两个弓形的面积;
问题3:求
:
的值.
 解:(1)DE与半圆O相切.
解:(1)DE与半圆O相切.证明:连接OD,BD,
∵AB是半圆O的直径,
∴∠BDA=∠BDC=90°.
∵在Rt△BDC中,E是BC边上的中点,
∴DE=BE=
| 1 |
| 2 |
∵OB=OD,
∴∠OBD=∠ODB.
又∵∠ABC=∠OBD+∠EBD=90°,
∴∠ODB+∠EDB=90°,故DE与半圆O相切.
(2)∵BD⊥AC,
∴Rt△ABD∽Rt△ACB.
∴
| AB |
| AC |
| AD |
| AB |
即AB2=AD•AC.
∴AC=
| AB2 |
| AD |
∵AD,AB的长是方程x2-10x+24=0的两个根,
∴解方程得x1=4,x2=6.
∵AD<AB,
∴AD=4,AB=6.
∴AC=
| AB2 |
| AD |
| 62 |
| 4 |
又∵在Rt△ABC中,AB=6,AC=9,
∴BC=
| AC2-AB2 |
| 81-36 |
| 5 |
(3)问题1:求四边形ABED的面积;
问题2:求两个弓形的面积;
问题3:求
 |
| AD |
 |
| BD |
点评:本题考查常见的几何题型,包括切线的判定,线段长度的求法,要求学生掌握常见的解题方法,并能结合图形选择简单的方法解题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD.
23、如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接ED、BD. 如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是
如图,以Rt△ABC各边为直径的三个半圆围成两个新月形(阴影部分),已知AC=3cm,BC=4cm.则新月形(阴影部分)的面积和是 已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.
已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD. 如图,以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D,若劣弧CD=120°,则
如图,以Rt△ABC的直角边AC为直径作圆O交斜边AB于点D,若劣弧CD=120°,则 (2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
(2009•黔南州)如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.