题目内容
（2009•黔南州）如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．（1）DE与半圆0是否相切？若相切，请给出证明；若不相切，请说明理由；
（2）若AD、AB的长是方程x2-16x+60=0的两个根，求直角边BC的长．
分析：（1）连接OD、BD，求出BD⊥AC，AD=CD，求出DE=BE，推出∠EDB=∠EBD，∠ODB=∠OBD，推出∠ODE=90°，根据切线的判定推出即可；
（2）求出AD和AB的值，证Rt△ADB∽Rt△ABC，得出
=
，求出AC=
，根据勾股定理求出即可．
（2）求出AD和AB的值，证Rt△ADB∽Rt△ABC，得出
| AB |
| AD |
| AC |
| AB |
| 50 |
| 3 |
解答：解：（1）DE与半圆O相切，理由如下：
连接OD、BD，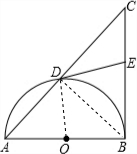
∵AB是⊙O的直径，
∴∠BDA=∠BDC=90°，
∵在Rt△BDC中，E为BC边上的中点，
∴DE=BE，
∴∠EBD=∠BDE，
∵OB=OD，
∴∠OBD=∠ODB，
∵∠ABC=∠OBD+∠EBD=90°，
∴∠ODB+∠EDB=90°，
∵OD是半径，
∴DE与半圆O相切；
（2）∵AD、AB的长是方程x2-16x+60=0的两个根，
∴解方程得：x1=6，x2=10，
∵AD＜AB，
∴AD=6，AB=10，
∵在Rt△ABC中，BD⊥AC，
∴Rt△ADB∽Rt△ABC，
∴
=
，
即AB2=AD•AC，
∴AC=
=
，
在Rt△ABC中，AB=10，AC=
，
∴BC=
=
．
连接OD、BD，
∵AB是⊙O的直径，
∴∠BDA=∠BDC=90°，
∵在Rt△BDC中，E为BC边上的中点，
∴DE=BE，
∴∠EBD=∠BDE，
∵OB=OD，
∴∠OBD=∠ODB，
∵∠ABC=∠OBD+∠EBD=90°，
∴∠ODB+∠EDB=90°，
∵OD是半径，
∴DE与半圆O相切；
（2）∵AD、AB的长是方程x2-16x+60=0的两个根，
∴解方程得：x1=6，x2=10，
∵AD＜AB，
∴AD=6，AB=10，
∵在Rt△ABC中，BD⊥AC，
∴Rt△ADB∽Rt△ABC，
∴
| AB |
| AD |
| AC |
| AB |
即AB2=AD•AC，
∴AC=
| AB2 |
| AD |
| 50 |
| 3 |
在Rt△ABC中，AB=10，AC=
| 50 |
| 3 |
∴BC=
| AC2-AB2 |
| 40 |
| 3 |
点评：本题考查了相似三角形的性质和判定，直角三角形斜边上中线性质，等腰三角形性质，圆周角定理，勾股定理等知识点的应用，主要考查学生的推理和计算能力．
练习册系列答案
相关题目
（2009•黔南州）如图，一架梯子斜靠在墙上，若梯子底端到墙的距离AC=3米，tan∠BCA=4：3，则梯子AB的长度为