Question

【题目】为了鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数y（台）与补贴款额x（元）之间大致满足如图①所示的一次函数关系．随着补贴款额x的不断增大，销售量也不断增加，但每台彩电的收益Z（元）会相应降低且Z与x之间也大致满足如图②所示的一次函数关系。

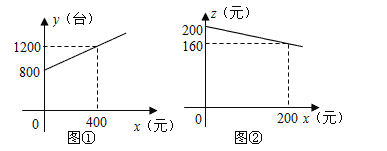
（1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？

（2）在政府补贴政策实施后，分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式；

（3）要使该商场销售彩电的总收益w（元）最大，政府应将每台补贴款额x定为多少并求出总收益w的最大值。

Answer 1

【答案】(1)160000元 (2)；；(3)100元时，w的最大值为162000元.

【解析】

试题分析：(1)根据图示可得未出台政策之前台数为800台，每台的收益为200元；(2)、利用待定系数法求出函数解析式；(3)、利用二次函数的性质求出最值.

试题解析：(1)、销售家电的总收益为800×200=160000（元）；

(2)依题意可设， ,

∴有 解得

所以 ；

(3)

∴政府应将每台补贴款额定为100元，总收益最大值，其最大值为162000元。