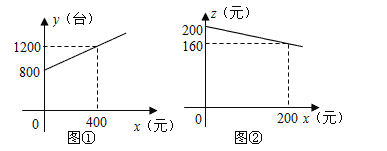
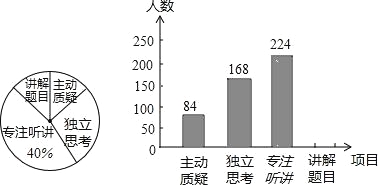
题目内容
【题目】已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA的延长线于点E,F. 当BE=CF时,求证:AE=AF.
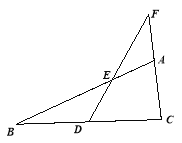
【答案】证明过程见解析
【解析】
试题分析:过点B作BG∥FC,延长FD交BG于点G,证明△BDG和△CDF全等,得到BG=CF,然后根据BE=CF,从而说明△BEG为等腰三角形,即∠G=∠BEG,根据平行可得∠G=∠F,根据对顶角可得∠BEG=∠AEF,根据等式的性质可得∠F=AEF,从而得出AE=AF.
试题解析:过点B作BG∥FC,延长FD交BG于点G.∴![]() . ∵点D是BC的中点,∴BD=CD.
. ∵点D是BC的中点,∴BD=CD.
在△BDG和△CDF中,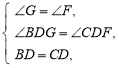 ∴ △BDG≌△CDF. ∴BG=CF. ∵BE=CF, ∴BE=BG.
∴ △BDG≌△CDF. ∴BG=CF. ∵BE=CF, ∴BE=BG.
∴∠G=∠BEG ∵∠BEG=∠AEF ∴∠G=∠AEF ∴∠F=∠AEF ∴AE=AF


练习册系列答案
相关题目