题目内容
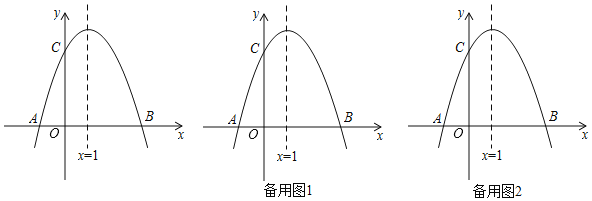
【题目】如图，已知抛物线y＝﹣x2+bx+c与x轴交于A、B两点，AB＝4，交y轴于点C，对称轴是直线x＝1．
（1）求抛物线的解析式及点C的坐标；
（2）连接BC，E是线段OC上一点，E关于直线x＝1的对称点F正好落在BC上，求点F的坐标；
（3）动点M从点O出发，以每秒2个单位长度的速度向点B运动，过M作x轴的垂线交抛物线于点N，交线段BC于点Q．设运动时间为t（t＞0）秒．
①若△AOC与△BMN相似，请直接写出t的值；
②△BOQ能否为等腰三角形？若能，求出t的值；若不能，请说明理由．
【答案】（1）y＝﹣x2+2x+3，C点坐标为(0，3)；（2）F(2，1)；（3）①t＝1；②当t
或
秒时，△BOQ为等腰三角形
【解析】
（1）将A、B关坐标代入y＝﹣x2+bx+c中，即可求解；
（2）确定直线BC的解析式为y＝﹣x+3，根据点E、F关于直线x＝1对称，即可求解；
（3）①△AOC与△BMN相似，则
，即可求解；②分OQ＝BQ、BO＝BQ、OQ＝OB三种情况，分别求解即可．
解：（1））∵点A、B关于直线x＝1对称，AB＝4，
∴A（﹣1，0），B（3，0），
代入y＝﹣x2+bx+c中，得：
，解得
，
∴抛物线的解析式为y＝﹣x2+2x+3，
∴C点坐标为（0，3）；
（2）设直线BC的解析式为y＝mx+n，
则有：
，解得
，
∴直线BC的解析式为y＝﹣x+3，
∵点E、F关于直线x＝1对称，
又E到对称轴的距离为1，
∴EF＝2，
∴F点的横坐标为2，将x＝2代入y＝﹣x+3中，
得：y＝﹣2+3＝1，
∴F（2，1）；
（3）①如下图，连接BC交MN于Q，
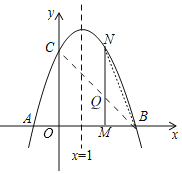
MN＝﹣4t2+4t+3，MB＝3﹣2t，
△AOC与△BMN相似，则，
即：
，
解得：t
或
或1（舍去
、），
故：t＝1；
②∵M（2t，0），MN⊥x轴，∴Q（2t，3﹣2t），
∵△BOQ为等腰三角形，∴分三种情况讨论，
第一种，当OQ＝BQ时，
∵QM⊥OB
∴OM＝MB
∴2t＝3﹣2t
∴t
；
第二种，当BO＝BQ时，在Rt△BMQ中
∵∠OBQ＝45°，
∴BQ
，
∴BO，
即3
，
∴t
；
第三种，当OQ＝OB时，
则点Q、C重合，此时t＝0
而t＞0，故不符合题意
综上述，当t或
秒时，△BOQ为等腰三角形．
