题目内容
已知一次函数y=kx+b的图象经过点(-1,-5),且与函数 的图象相交于点
的图象相交于点 .
.(1)求a的值;
(2)求不等式组
 的正整数解;
的正整数解;(3)若函数y=kx+b图象与x轴的交点是B,函数
 的图象与y轴的交点是C,求四边形ABOC的面积.
的图象与y轴的交点是C,求四边形ABOC的面积.
【答案】分析:(1)将点代入可得出a的值.
(2)求出函数解析式,得到不等式,就能解决.
(3)将面积分解就可得出答案.
解答:解:(1)把( ,a)代入解析式y=
,a)代入解析式y= x+1,
x+1,
得到: ;
;
(2)由(1)得k=2,b=-3,
∴ ,
,
解得: ,
,
∴正整数解为x=2;
(3)直线 与y轴交于点C(0,1),
与y轴交于点C(0,1),
直线y=2x-3与x轴交于点 ,
,
∴ .
.
点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.正确作出图象,把求线段的长度的问题转化为求点的坐标的问题.
(2)求出函数解析式,得到不等式,就能解决.
(3)将面积分解就可得出答案.
解答:解:(1)把(
 ,a)代入解析式y=
,a)代入解析式y= x+1,
x+1,得到:
 ;
;(2)由(1)得k=2,b=-3,
∴
 ,
,解得:
 ,
,∴正整数解为x=2;
(3)直线
 与y轴交于点C(0,1),
与y轴交于点C(0,1),直线y=2x-3与x轴交于点
 ,
,∴
 .
.点评:本题考查了一次函数与不等式(组)的关系及数形结合思想的应用.正确作出图象,把求线段的长度的问题转化为求点的坐标的问题.

练习册系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.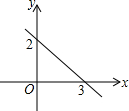 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.