题目内容
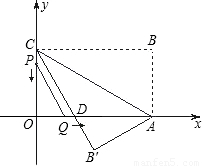
已知矩形OABC的边长OA=4,AB=3,E是OA的中点,分别以所在的直线为x轴,y轴,建立如图所示的平面直角坐标系,直线l经过C、E两点.
(1)求直线l的函数表达式;
(2)如图,将矩形OABC中,将△COE沿直线l折叠后得到△CFE,点F在矩形OABC内部,延长CF交AB于G点.证明:GF=GA;
(3)由上面的条件,求四边形AGFE的面积?

(1)求直线l的函数表达式;
(2)如图,将矩形OABC中,将△COE沿直线l折叠后得到△CFE,点F在矩形OABC内部,延长CF交AB于G点.证明:GF=GA;
(3)由上面的条件,求四边形AGFE的面积?

分析:(1)易求E(2,0),C(0,3).把点E、C的坐标代入直线l的解析式y=kx+b(k≠0),列出关于k、b的方程组,通过解方程组可以求得它们的值;
(2)如图2,连接EG.通过证明Rt△EFG≌Rt△EAG来证明GF=GA;
(3)根据矩形的性质、折叠的性质以及(2)中全等三角形的性质推知BG=AB-AG=3-AG,CG=CF+GF=3+GA,AE=2.则在直角△CBG中,由勾股定理求得AG=
.
所以有全等三角形的性质得到S四边形AGFE=2SRt△EAG=2×
AE•AG=
.
(2)如图2,连接EG.通过证明Rt△EFG≌Rt△EAG来证明GF=GA;
(3)根据矩形的性质、折叠的性质以及(2)中全等三角形的性质推知BG=AB-AG=3-AG,CG=CF+GF=3+GA,AE=2.则在直角△CBG中,由勾股定理求得AG=
| 4 |
| 3 |
所以有全等三角形的性质得到S四边形AGFE=2SRt△EAG=2×
| 1 |
| 2 |
| 8 |
| 3 |
解答: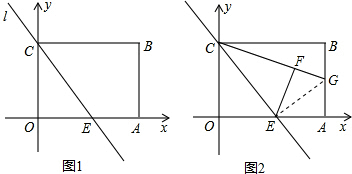 (1)解:设直线l的解析式y=kx+b(k≠0).
(1)解:设直线l的解析式y=kx+b(k≠0).
∵矩形OABC的边长OA=4,AB=3,E是OA的中点,
∴OC=AB=3,OE=2,
∴E(2,0),C(0,3).
∴
,
解得,
,
∴直线l的解析式y=-
x+3;
(2)证明:如图2,连接EG.
∵四边形OABC是矩形,
∴∠COA=∠OAB=90°.
又根据折叠是性质得到∠COE=∠CFE=90°,OE=EF,
∴∠EFG=∠EAG=90°.
又∵E是OA的中点,
∴OE=EF,
∴EF=EA,
∴在Rt△EFG和Rt△EAG中,
,
∴Rt△EFG≌Rt△EAG(HL),
∴GF=GA;
(3)解:由(2)知,GF=GA,根据折叠的性质知OC=CF=3.
∵BG=AB-AG=3-AG,CG=CF+GF=3+GA,AE=2,
∴在直角△CBG中,由勾股定理得:CG2=BC2+BG2,即(3+AG)2=(3-AG)2+42,
解得,AG=
.
∵由(1)知,Rt△EFG≌Rt△EAG,
∴SRt△EFG=SRt△EAG,
∴S四边形AGFE=2SRt△EAG=2×
AE•AG=2×
×2×
=
,即四边形AGFE的面积是
.
 (1)解:设直线l的解析式y=kx+b(k≠0).
(1)解:设直线l的解析式y=kx+b(k≠0).∵矩形OABC的边长OA=4,AB=3,E是OA的中点,
∴OC=AB=3,OE=2,
∴E(2,0),C(0,3).
∴
|
解得,
|
∴直线l的解析式y=-
| 3 |
| 2 |
(2)证明:如图2,连接EG.
∵四边形OABC是矩形,
∴∠COA=∠OAB=90°.
又根据折叠是性质得到∠COE=∠CFE=90°,OE=EF,
∴∠EFG=∠EAG=90°.
又∵E是OA的中点,
∴OE=EF,
∴EF=EA,
∴在Rt△EFG和Rt△EAG中,
|
∴Rt△EFG≌Rt△EAG(HL),
∴GF=GA;
(3)解:由(2)知,GF=GA,根据折叠的性质知OC=CF=3.
∵BG=AB-AG=3-AG,CG=CF+GF=3+GA,AE=2,
∴在直角△CBG中,由勾股定理得:CG2=BC2+BG2,即(3+AG)2=(3-AG)2+42,
解得,AG=
| 4 |
| 3 |
∵由(1)知,Rt△EFG≌Rt△EAG,
∴SRt△EFG=SRt△EAG,
∴S四边形AGFE=2SRt△EAG=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
点评:本题综合考查了待定系数法求一次函数的解析式,折叠的性质,矩形的性质,勾股定理以及全等三角形的判定与性质.考查了同学们综合运用所学知识的能力,是一道综合性较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010•来宾)已知矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒.
(2010•来宾)已知矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正半轴上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点到达终点时,另一点即停止运动.设运动的时间为t秒. A、C两点分别在x轴、y轴上.将△ABC沿AC翻折,点B落到B′处,B′C交x轴于点D,且sin∠OCD=
A、C两点分别在x轴、y轴上.将△ABC沿AC翻折,点B落到B′处,B′C交x轴于点D,且sin∠OCD=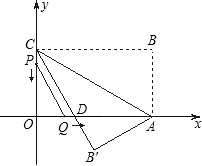 A、C两点分别在x轴、y轴上.将△ABC沿AC翻折,点B落到B′处,B′C交x轴于点D,且sin∠OCD=
A、C两点分别在x轴、y轴上.将△ABC沿AC翻折,点B落到B′处,B′C交x轴于点D,且sin∠OCD= .
. .
.