题目内容
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,点D为BC的中点,点E,F分别在直线AB,AC上运动,且始终保持AE=CF.
(1)如图①,若点E,F分别在线段AB,AC上,求证:DE=DF且DE⊥DF; 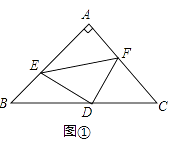
(2)如图②,若点E、F分别在线段AB,CA的延长线上,(1)中的结论是否依然成立?说明理由. 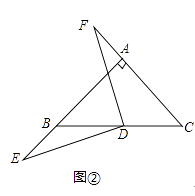
【答案】
(1)解:如图①,连接AD,
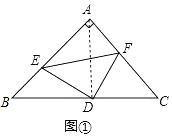
∵∠BAC=90°,AB=AC,D为BC中点,
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
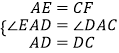 ,
,
∴△AED≌△CFD(SAS),
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF+∠ADF=90°,
∴∠ADE+∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF
(2)解:若点E,F分别在线段AB,CA的延长线上,(1)中的结论依然成立,如图②,
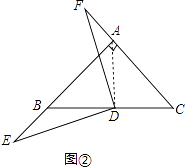
理由:∵∠BAC=90° AB=AC,D为BC中点
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
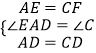 ,
,
∴△AED≌△CFD(SAS);
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF﹣∠ADF=90°,
∴∠ADE﹣∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF
【解析】(1)利用等腰直角三角形的性质得出AD=BD=DC,进而证明△AED≌△CFD,利用全等三角形的性质得出DE=DF,∠ADE=∠CDF进而得出△DEF为等腰直角三角形;(2)若点E、F分别在线段AB,CA的延长线上,(1)中的结论依然成立,首先利用已知得出AD=BD=DC,进而利用全等三角形的判定得出△AED≌△CFD.
【考点精析】通过灵活运用等腰直角三角形,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°即可以解答此题.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案