Question

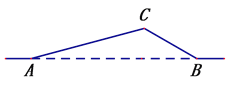
【题目】如图，从A地到B地的公路需经过C地，图中AC=6千米，∠CAB=15°，∠CBA=30°. 因城市规划的需要，将在A、B两地之间修建一条笔直的公路.

（1）求改直后的公路AB的长；

（2）问公路改直后该段路程比原来缩短了多少千米？（结果保留根号）

Answer 1

【答案】（1）改直后的公路AB的长为6千米；

(2) 公路改直后该段路程比原来缩短了（6+3－9）千米。

【解析】试题分析：（1）过点A作AD⊥BC交BC的延长线于点D，在Rt△ACD中，利用三角函数求解即可；

（2）根据（1）中的结论，求出BC的长，根据公路比原来缩短距离为AC+BC-AB求解即可.

试题解析：（1）过点A作AD⊥BC交BC的延长线于点D，∵∠B=30°，∠CAB=15°，∴∠ACD=45°. 在RtACD中，∠ADC=90°，∠ACD=45°，AC=6，∴CD=AD=3 .在RtABD中，∠ADB=90°，∠B=30°，AD=3，∴AB=6，答：改直后的公路AB的长为6千米；

(2) 在RtABD中，∠ADB=90°，∠B=30°，AD=3，∴BD=3∴BC=3－3,

AC+BC-AB=6+3－3-6=6+3－9

答：公路改直后该段路程比原来缩短了（6+3－9）千米。