题目内容
（推理填空）如图所示，点O是直线AB上一点，∠BOC=130°，OD平分∠AOC．求：∠COD的度数．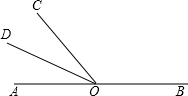
解：∵O是直线AB上一点∴∠AOB=
∵∠BOC=130°
∴∠AOC=∠AOB-∠BOC=
∵OD平分∠AOC
∴∠COD=
| 1 | 2 |
分析：根据平角和角平分线的定义求解，根据解题步骤填上适当的数．
解答：解：∵O是直线AB上一点
∴∠AOB=180°．
∵∠BOC=130°
∴∠AOC=∠AOB-∠BOC=50°．
∵OD平分∠AOC
∴∠COD=
∠AOC=25°．
故答案为180°、50°、∠AOC、25°．
∴∠AOB=180°．
∵∠BOC=130°
∴∠AOC=∠AOB-∠BOC=50°．
∵OD平分∠AOC
∴∠COD=
| 1 |
| 2 |
故答案为180°、50°、∠AOC、25°．
点评：根据角平分线定义得出所求角与已知角的关系转化求解．
练习册系列答案
相关题目
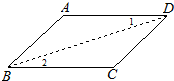24、完成推理填空：如图所示，已知AD=BC，AB=DC，试判断∠A与∠ABC的关系．下面是小颖同学的推导过程：
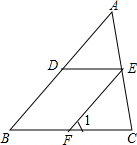推理填空．如图所示．因为∠1=∠DEF（已知）．所以
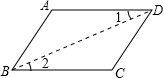解：连接BD．在△ABD与△CDB中
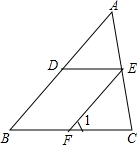推理填空．如图所示．因为∠1=∠DEF（已知）．所以________∥________；因为∠1=________（已知）．所以________∥________（同位角相等，两直线平行）；因为∠B+________=180°（已知），所以DE∥BC________．