题目内容
推理填空．如图所示．因为∠1=∠DEF（已知）．所以DE
DE
∥BC
BC
；因为∠1=∠B
∠B
（已知）．所以EF
EF
∥AB
AB
（同位角相等，两直线平行）；因为∠B+∠BDE
∠BDE
=180°（已知），所以DE∥BC同旁内角互补，两直线平行
同旁内角互补，两直线平行
．分析：根据平行线的判定定理进行填空．
解答：解：如图所示．∵∠1=∠DEF（已知）．
∴DE∥BC；因为∠1=∠B（已知）．
∴EF∥AB（同位角相等，两直线平行）；
∵∠B+BDE=180°（已知），
∴DE∥BC （同旁内角互补，两直线平行）．
故答案是：DE，BC，∠B，EF，AB，∠BDE，同旁内角互补，两直线平行．
∴DE∥BC；因为∠1=∠B（已知）．
∴EF∥AB（同位角相等，两直线平行）；
∵∠B+BDE=180°（已知），
∴DE∥BC （同旁内角互补，两直线平行）．
故答案是：DE，BC，∠B，EF，AB，∠BDE，同旁内角互补，两直线平行．
点评：本题考查了平行线的判定．解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角．
练习册系列答案
相关题目
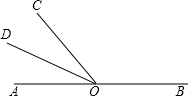解：∵O是直线AB上一点
24、完成推理填空：如图所示，已知AD=BC，AB=DC，试判断∠A与∠ABC的关系．下面是小颖同学的推导过程：
解：连接BD．在△ABD与△CDB中
推理填空．如图所示．因为∠1=∠DEF（已知）．所以________∥________；因为∠1=________（已知）．所以________∥________（同位角相等，两直线平行）；因为∠B+________=180°（已知），所以DE∥BC________．