题目内容
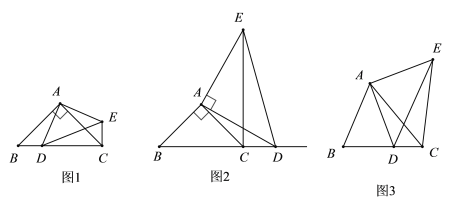
【题目】已知:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.求证:①△ADC≌△CEB;②DE=AD﹣BE.
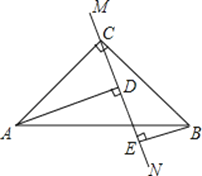
【答案】证明见解析
【解析】
①根据垂直定义求出∠BEC=∠ACB=∠ADC,根据等式性质求出∠ACD=∠CBE,根据AAS证出△ADC和△CEB全等即可;
②由①推出AD=CE,CD=BE,即可推出答案.
证明:①∵∠ACB=90°,BE⊥CE,AD⊥CE,
∴∠BEC=∠ACB=∠ADC=90°,
∴∠ACE+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中
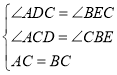
∴△ADC≌△CEB(AAS).
②∵△ADC≌△CEB,
∴AD=CE,BE=CD,
∴CECD=ADBE,
∵DE=CECD,
∴DE=ADBE.

练习册系列答案
相关题目
【题目】在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为![]() ,
, ![]() .下列说法:
.下列说法:
①两组的平均数相同;
②甲组学生成绩比乙组学生成绩稳定;
③甲组成绩的众数>乙组成绩的众数;
④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.其中正确的共有( )
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
A. 2种 B. 3种 C. 4种 D. 5种