题目内容
【题目】如图,在△ABC中,∠ABC为锐角,点D为直线BC上一动点,以AD为直角边且在AD的右侧作等腰直角三角形ADE,∠DAE=90°,AD=AE.
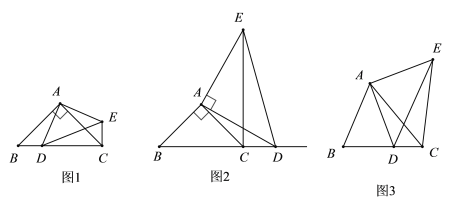
(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时,如图1,线段CE、BD的位置关系为___________,数量关系为___________
②当点D在线段BC的延长线上时,如图2,①中的结论是否仍然成立,请说明理由.
(2)如图3,如果AB≠AC,∠BAC≠90°,点D在线段BC上运动。探究:当∠ACB多少度时,CE⊥BC?请说明理由.
【答案】(1)①垂直,相等.②都成立,理由见解析;(2)45°,理由见解析
【解析】
试题(1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;
(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.
试题解析:
解(1):(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为:垂直,相等;
②都成立,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,

∴△DAB≌△EAC,
∴CE=BD,∠B=∠ACE,
∴∠ACB+∠ACE=90°,即CE⊥BD;
(2)当∠ACB=45°时,CE⊥BD(如图).
理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,

∵∠ACB=45°,∠AGC=90°﹣∠ACB,
∴∠AGC=90°﹣45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
在△GAD与△CAE中,

∴△GAD≌△CAE,
∴∠ACE=∠AGC=45°,
∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥BC.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案