题目内容
【题目】如图,将边长分别为6,2 ![]() 的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是(只填序号)
的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是(只填序号)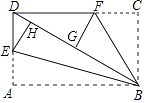
【答案】①②
【解析】解:①∵由折叠的性质得,∠ABE=∠DBE,∠DBF=∠CBF,
∴∠DBE+∠DBF=∠ABE+∠CBF= ![]() ∠ABC,
∠ABC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠EBF=∠EBD+∠FBD=45°,
故①正确;②∵AB=6,AD=2 ![]() ,
,
∴tan∠ABD= ![]() =
= ![]() ,
,
∴∠ABD=30°,
∠BDC=30°,
∴∠CBD=60°,
∴∠DBF= ![]() ∠CBD=30°,
∠CBD=30°,
∴∠FDB=∠FBD,
∴DF=BF,
∵∠C=90°,∠BDC=30°,
∴CE= ![]() BD,
BD,
由折叠的性质得,BG=BC,
∴DG=BG,
∴FG⊥BD,
∴FG是BD的垂直平分线;故②正确;
∵∠CBF=∠FBD=30°,∠C=90°,
∴CF= ![]() BC=3,
BC=3,
∴DF=CD﹣CF=4,故③错误.
所以答案是:①②.
【考点精析】掌握线段垂直平分线的性质和矩形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;矩形的四个角都是直角,矩形的对角线相等.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康.在2017年2月周末休息期间,某校九年级一班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计表及统计图,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
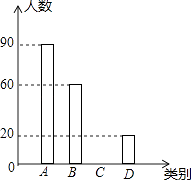
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若该市有800万人口,请你估计持有B,C两类看法的市民共有多少人?
(3)小明同学在四个质地、大小、形状都完全相同的小球上标记A,B,C,D代表四个雾霾天气的主要成因中,放在一个不透明的盒子中,他先随机抽取一个小球,放回去,再随机抽取一个小球,请用画树状图或列表的方法,求出小颖同学刚好抽到B和D的概率.(用A,B,C,D表示各项目)
【题目】某农户以1500元/亩的单价承包了15亩地种植板栗,每亩种植80株优质板栗嫁接苗,购买嫁接苗,购买价格为5元/株,且每亩地的管理费用为800元,一年下来喜获丰收平均每亩板栗产量为600kg,已知当地板栗的批发和;零售价格分别如下表所示:
销售方式 | 批发 | 零售 |
售价(元/kg) | 10 | 14 |
通过市场调研发现,批发与零售的总销量只能达到总产量的70%,其中零售量不高于总销售量的40%,经多方协调当地食品加工厂承诺以7元/kg的价格收购该农户余下的板栗,设板栗全部售出后的总利润为y元,其中零售x kg.
(1)求y与x之间的函数关系
(2)求该农户所收获的最大利润
(总利润=总销售额-总承包费用-购买板栗苗的费用-总管理费用)